TANGENCIAS
La palabra tangente proviene del latín “tangens” que significa “que toca”, esto es, que tiene un punto en común sin cortarse.
1. RECTA TANGENTE A UNA CIRCUNFERENCIA EN UNO DE SUS PUNTOS.
Para que una recta sea tangente a una circunferencia en uno de sus puntos ha de ser perpendicular al radio de circunferencia que pasa por ese punto.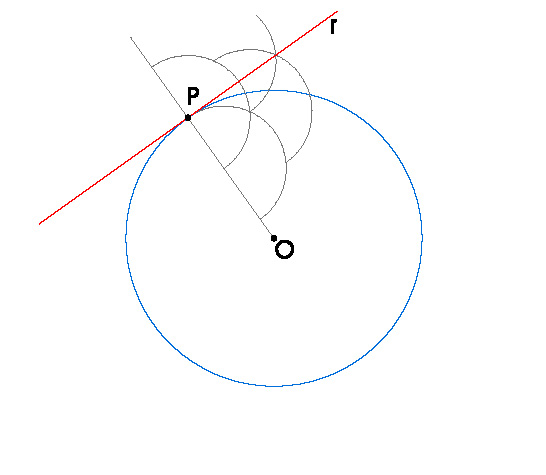 PASOS:
PASOS:
 PASOS:
PASOS:- Dibujamos la circunferencia a la que vamos a trazar la tangente y llamamos a su centro O.
- Marcamos un punto P en la circunferencia por el que vamos a trazar la tangente.
- Dibujamos el radio O P.
- Dibujamos la perpendicular al segmento OP que pase por P.
- Esa recta “r” será nuestra tangente buscada.
2. RECTAS TANGENTES A UNA CIRCUNFERENCIA QUE PASEN POR UN PUNTO P EXTERIOR A LA MISMA.
Al intentar trazar las rectas tangentes a una circunferencia que pasen por un punto P exterior a la misma, observamos que el problema tiene dos posibles soluciones. La solución de este problema se fundamenta en dos cuestiones:
- El hecho de que la tangente a una circunferencia en un punto es perpendicular al radio en ese punto, por lo que los triángulos POT1 y POT2 son dos triángulos rectángulos.
- El concepto de arco capaz de un segmento para un ángulo determinado, que es el lugar geométrico de los puntos del plano desde los que vemos el segmento con ese ángulo.
En nuestro caso queremos ver el segmento OP con un ángulo de 90º, para ello, dibujamos la circunferencia de la que OP es un diámetro (un ángulo central de 180º) por lo tanto, los ángulos inscritos que dibujemos que abarquen ese ángulo central serán de 90º. Arco capaz del ángulo de 90º
Arco capaz del ángulo de 90º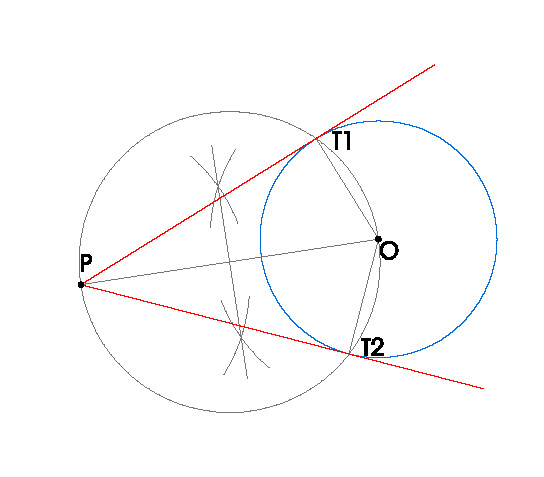 PASOS:
PASOS:
 Arco capaz del ángulo de 90º
Arco capaz del ángulo de 90º PASOS:
PASOS:- Dibujamos una circunferencia y llamamos a su centro O.
- Dibujamos un punto P, cualquiera, exterior a la circunferencia, desde el que haremos las tangentes.
- Unimos O con P.
- Hacemos la mediatriz del segmento OP.
- Con centro en el punto medio del segmento OP, dibujamos la circunferencia que pasa por O y P.
- Donde esa circunferencia nos corte a la circunferencia inicial obtenemos los puntos de tangencia T1 y T2.
- Uniendo P con T1 y T2 obtenemos las dos tangentes buscadas.
3. CIRCUNFERENCIAS TANGENTES A TRES RECTAS QUE SE CORTAN.
Las circunferencias pedidas son las exinscritas al triángulo que forman las tres rectas. Sus centros son los puntos de intersección de las bisectrices de los ángulos exteriores del triángulo. Este sería el tercero de los diez problemas de Apolonio, que tendría una solución más, que sería la circunferencia inscrita al triángulo formado por las tres rectas. Para resolver este ejercicio debemos recordar el concepto de bisectriz. La bisectriz es el lugar geométrico de los puntos del plano que equidistan de los lados de un ángulo, y por tanto, como vimos al construir el incentro de un triángulo, es el centro de todas las circunferencias tangentes a los lados del ángulo.
La bisectriz es el lugar geométrico de los puntos del plano que equidistan de los lados de un ángulo, y por tanto, como vimos al construir el incentro de un triángulo, es el centro de todas las circunferencias tangentes a los lados del ángulo. PASOS:
PASOS:
 La bisectriz es el lugar geométrico de los puntos del plano que equidistan de los lados de un ángulo, y por tanto, como vimos al construir el incentro de un triángulo, es el centro de todas las circunferencias tangentes a los lados del ángulo.
La bisectriz es el lugar geométrico de los puntos del plano que equidistan de los lados de un ángulo, y por tanto, como vimos al construir el incentro de un triángulo, es el centro de todas las circunferencias tangentes a los lados del ángulo. PASOS:
PASOS:- Dibujamos las tres rectas a las que vamos a calcular las circunferencias tangentes.
- Para calcular el centro O1, hacemos las dos bisectrices de los ángulos que forman las tres rectas y donde se corten obtenemos O1.
- Una vez obtenido O1, para calcular los puntos de tangencia, hacemos las perpendiculares a las rectas obteniendo T1 y T2.
- Para calcular el centro O2, sólo tenemos que hacer una bisectriz, puesto que la otra es la misma que la del ángulo opuesto ya calculada previamente.
- Una vez obtenido el centro O2, calculamos sus puntos de tangencia T3 y T4, haciendo las perpendiculares a las rectas que pasen por O2.
- Para obtener el centro O3, sólo tenemos que prolongar las bisectrices ya dibujadas.
- Una vez obtenido el centro O3, calculamos sus puntos de tangencia T5 y T6, haciendo las perpendiculares a las rectas que pasen por O3.
4. CIRCUNFERENCIA TANGENTE A UNA RECTA DADA EN UN PUNTO DE ESTA “T” Y QUE PASE POR UN PUNTO TAMBIÉN DADO “P”.
Para calcular la solución de este ejercicio, debemos recordar el concepto de mediatriz, que es el lugar geométrico de los puntos del plano que equidistan de los extremos del segmento del que es mediatriz, y por tanto es el centro de todas las circunferencias que pasan por los dos extremos del segmento.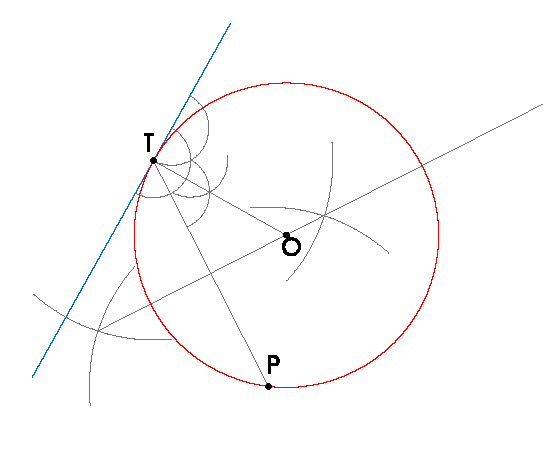 PASOS:
PASOS:
 PASOS:
PASOS:- Unimos el punto P, dado, con el punto T, también dado.
- Hacemos la mediatriz del segmento PT, y por tanto es el centro de todas las circunferencias que pasan por los puntos P y T .
- También sabemos, que si una circunferencia es tangente a una recta en un punto, esa recta es perpendicular al radio de circunferencia que pasa por ese punto, por tanto, de todos los puntos de la mediatriz, sólo nos servirá como centro de la circunferencia buscada, áquel que esté en la perpendicular a la recta dada que pase por T.
- Hacemos la perpendicular a la recta que pase por T, donde nos corte a la mediatriz del segmento PT, obtenemos el punto O, centro de la circunferencia buscada.
5. RECTAS TANGENTES INTERIORES A DOS CIRCUNFERENCIAS.
 PASOS:
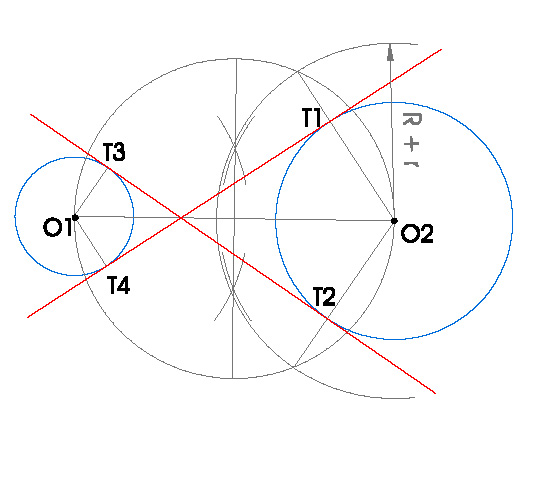
PASOS:- Dibujamos dos circunferencias O1 y O2, a las que vamos a realizar las tangentes.
- Unimos sus centros O1 y O2 y hacemos la mediatriz del segmento O1O2, para dibujar una circunferencia que pase por O1 y O2.
- Hacemos una circunferencia de centro O2, en nuestro caso la circunferencia mayor, y radio la suma de los radios de las dos circunferencias.
- Esta circunferencia nos corta a la dibujada previamente que pasa por O1 y O2 en dos puntos, uniendo esos dos puntos con O2, obtenemos los puntos de tangencia T1 y T2.
- Para calcular los puntos de tangencia T3 y T4, hacemos paralelas a los radios O2T1 y O2T2 que pasen por O1.
- Uniendo T1 con T4 y T2 con T3 obtenemos las tangentes buscadas.
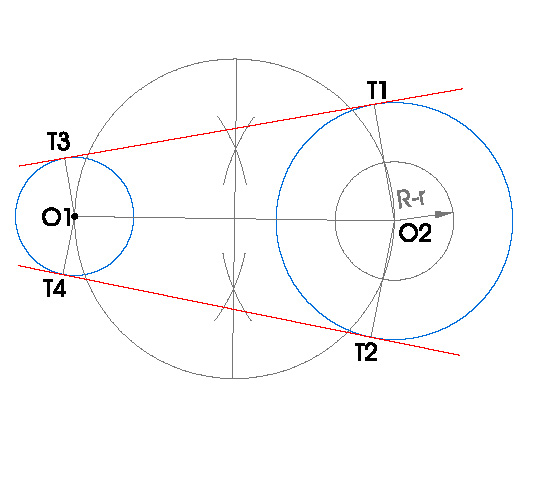
6. RECTAS TANGENTES EXTERIORES A DOS CIRCUNFERENCIAS.
 PASOS:
PASOS:- Dibujamos dos circunferencias O1 y O2, a las que vamos a realizar las tangentes.
- Unimos sus centros O1 y O2 y hacemos la mediatriz del segmento O1O2, para dibujar una circunferencia que pase por O1 y O2.
- Hacemos una circunferencia de centro O2, en nuestro caso la circunferencia mayor, y radio la resta de los radios de las dos circunferencias.
- Esta circunferencia nos corta a la dibujada previamente que pasa por O1 y O2 en dos puntos, uniendo esos dos puntos con O2, obtenemos los puntos de tangencia T1 y T2.
- Para calcular los puntos de tangencia T3 y T4, hacemos paralelas a los radios O2T1 y O2T2 que pasen por O1.
- Uniendo T1 con T3 y T2 con T4 obtenemos las tangentes buscadas.
ENLACES.
PASOS:
PASOS:
PASOS:
PASOS:
PASOS:

PASOS:
PASOS:
Enlace es la unión armónica de dos o más líneas curvas o rectas y curvas entre sí, por medio detangencias.
En el enlace entre un arco de circunferencia y una recta, el radio del arco perpendicular a la rectadetermina en su intersección con esta el punto de tangencia entre ambas.
El enlace entre dos arcos tiene siempre su punto de tangencia en línea recta con los centros de ambos arcos.
En el enlace entre un arco de circunferencia y una recta, el radio del arco perpendicular a la rectadetermina en su intersección con esta el punto de tangencia entre ambas.
El enlace entre dos arcos tiene siempre su punto de tangencia en línea recta con los centros de ambos arcos.
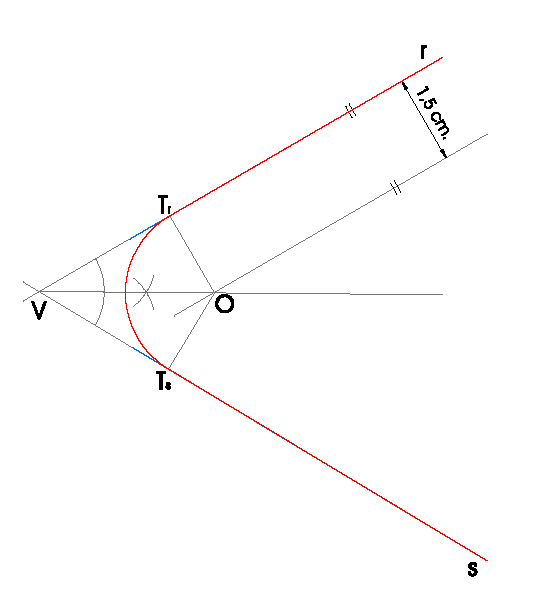
1. UNIR DOS RECTAS r Y s, SECANTES, MEDIANTE UN ARCO DE CIRCUNFERENCIA DE RADIO r = 1,5 cm.

PASOS:
- Una vez dibujadas las rectas r y s, las prolongamos hasta que se corten en un punto V.
- Hacemos la bisectriz del ángulo formado por r y s con vértice en V.
- Dibujamos una paralela a una de las rectas a una distancia del radio con el que queremos realizar el enlace, en nuestro caso 1,5 cm.
- Donde esa recta nos corte a la bisectriz, es el centro del arco de enlace O.
- Para calcular los puntos de tangencia de ese arco en las rectas ry s, Ts y Tr, debemos realizar dos perpendiculares desde O hasta r y hasta s.
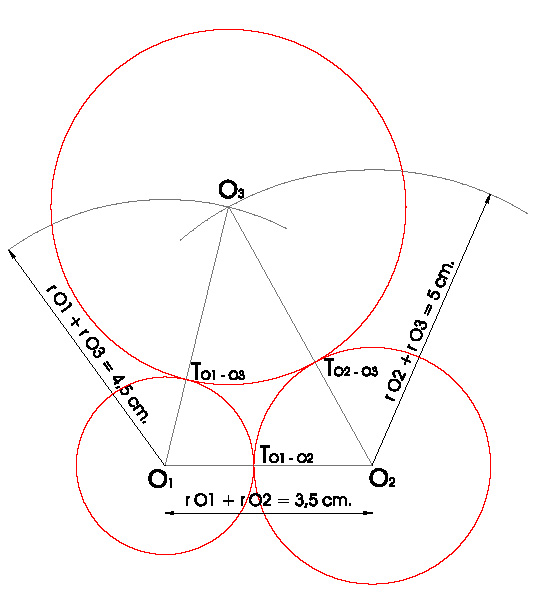
2. DIBUJAR TRES CIRCUNFERENCIAS TANGENTES ENTRE SÍ DE RADIOS: r1 = 1,5 cm., r2 = 2 cm. y r3 = 3 cm.

PASOS:
- Lo primero que tenemos que hacer es fijar uno de los centros O1.
- Desde O1, dibujamos un segmento de longitud la suma de los radios de O1 y O2, en nuestro caso 1,5 cm. más 2 cm., en total 3,5 cm. obteniendo O2.
- Desde O1 hacemos un arco de circunferencia con radio la suma de los radios de O1 y O3, en nuestro caso, 1,5 cm. más 3 cm., en total 4,5 cm.
- Desde O2 hacemos un arco de circunferencia con radio la suma de los radios de O2 y O3, en nuestro caso, 2 cm. más 3 cm., en total 5 cm.
- Donde se nos corten esos dos arcos obtenemos O3.
- Ya podemos dibujar las tres circunferencias tangentes con los radios dados.
3. UNIR DOS CIRCUNFERENCIAS DADAS O1 DE RADIO r1 = 2 cm. y O2 DE RADIO 2,5 cm. MEDIANTE UN ARCO DE CIRCUNFERENCIA DE RADIO r = 3 cm.
este ejercicio tiene dos soluciones.

PASOS:

PASOS:
- Dibujamos las dos circunferencias O1 y O2 con los radios dados.
- Con centro en O1 dibujamos dos arcos de circunferencia de radio la suma del radio de O1 y el del arco de circunferencia con el que queremos empalmar las circunferencias, en nuestro caso, 2 cm. más 3 cm., en total 5 cm.
- Con centro en O2 dibujamos dos arcos de circunferencia de radio la suma del radio de O2 y el del arco de circunferencia con el que queremos empalmar las circunferencias, en nuestro caso, 2,5 cm. más 3 cm., en total 5,5 cm.
- Donde se nos cortan los arcos de circunferencia obtenemos O3 y O4 que serán los centros de los arcos con los que empalmaremos O1 y O2.
- Para calcular los puntos de tangencia, lo único que tenemos que hacer es unir O3 y O4 con O1 y O2.
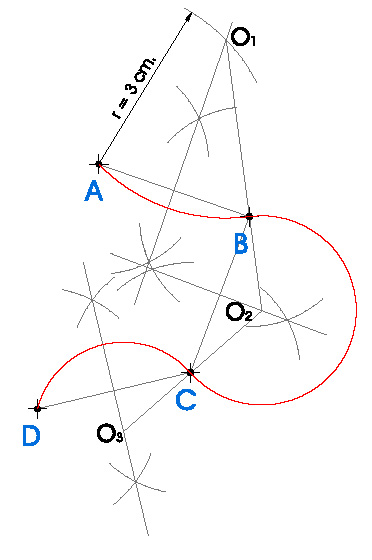
4. EMPALMAR POR MEDIO DE ARCOS DE CIRCUNFERENCIA CUATRO PUNTOS NO ALINEADOS A, B, C Y D CONOCIDO EL RADIO DEL PRIMER ENLACE r = 3 cm.

PASOS:
- Dibujamos los puntos A, B, C y D.
- Unimos A con B y hacemos la mediatriz del segmento AB.
- Dibujamos un arco de circunferencia con radio 3 cm. y donde nos corte a la mediatriz obtenemos el primer centro para hacer nuestros enlaces O1.
- Dibujamos un arco de circunferencia con centro O1 y radio 3 cm.
- Unimos B con C y hacemos la mediatriz del segmento BC.
- Unimos O1 con B y donde nos corte a la mediatriz dibujada obtenemos nuestro segundo centro O2.
- Dibujamos un arco de circunferencia con centro O2 y radio hasta B o C.
- Unimos C con D y hacemos la mediatriz del segmento CD.
- Unimos O2 con C y donde nos corte a la mediatriz dibujada obtenemos nuestro tercer centro O3.
- Dibujamos un arco de circunferencia con centro O3 y radio hasta C o D.
Para la realización de los ejercicios propuestos en ésta práctica debemos repasar conceptos como el deLugar Geométrico y el de bisectriz.
La correcta resolución de estos ejercicios depende en gran medida de la exactitud y limpieza con que los realicemos, así que tratad de realizarlos lo más cuidadosamente posible.
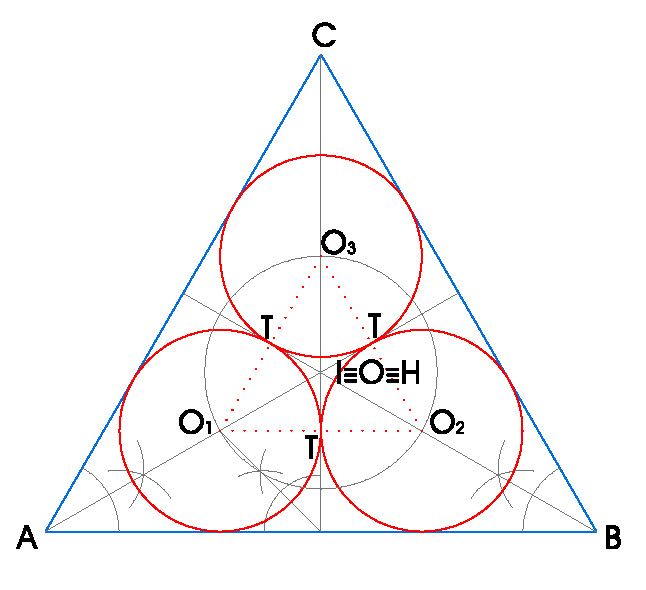
1. DIBUJA TRES CIRCUNFERENCIAS INSCRITAS EN UN TRIÁNGULO EQUILÁTERO DE LADO 7 cm. TANGENTES ENTRE SI.

PASOS:
- Dibujamos un triángulo equilátero de lado 7 cm.
- Calculamos su incentro, como queremos dibujar circunferencias tangentes a los lados del triángulo, sabemos que sus centros estarán situados en las bisectrices de los ángulos del triángulo.
- Por ser un triángulo equilátero, las bisectrices de sus ángulos coinciden con sus alturas. Las circunferencias interiores tendrán sus puntos de tangencia situados en esas alturas.
- Hallamos la bisectriz del ángulo formado entre una de las alturas y uno de los lados del triángulo.
- Donde la bisectriz se nos corte con la bisectriz del ángulo contiguo, obtenemos el primero de los centros de las circunferencias solución O1.
- Los otros dos centros de circunferencia, O2 y O3, estarán a la misma distancia del incentro que O1, con lo que si trazamos una circunferencia de radio IO1, donde nos corte a las bisectrices de los ángulos del triángulo obtenemos O2 y O3.
- Además sabemos que si dos circunferencias son tangentes en un punto, necesariamente ese punto estará en el segmento que une sus centros, así que si unimos O1, O2 y O3, obtendremos los puntos de tangencia T de las tres circunferencias, por lo que sabremos sus radios y podremos dibujarlas.
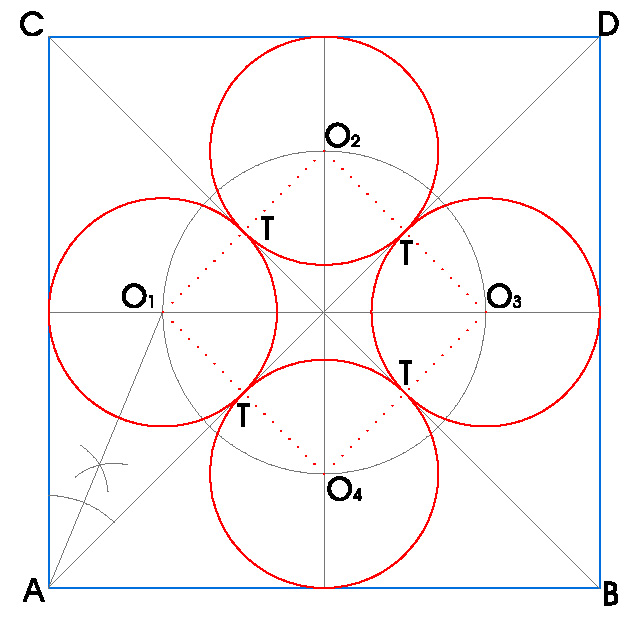
2. DIBUJA CUATRO CIRCUNFERENCIAS INSCRITAS EN UN CUADRADO DE LADO 7 cm. TANGENTES ENTRE SI Y A LAS DIAGONALES DEL CUADRADO.

PASOS:
- Dibujamos un cuadrado de lado 7 cm.
- Dibujamos sus diagonales, a las que deberán ser tangentes las circunferencias solución.
- Dibujamos las bisectrices de los ángulos formados por las diagonales, por ser un cuadrado, coinciden con los segmentos resultantes de hacer perpendiculares a los lados que pasen por el punto de corte de las diagonales, en estas bisectrices estarán los centros de las circunferencias solución..
- Hallamos la bisectriz del ángulo formado entre una diagonal y uno de los lados, donde se nos corte con la bisectriz realizada anteriormente obtendremos O1.
- O2, O3 y O4, estarán a la misma distancia del punto de corte de las diagonales que O1.
- Además sabemos que si dos circunferencias son tangentes en un punto, necesariamente ese punto estará en el segmento que une sus centros, así que si unimos O1, O2, O3 y O4, obtendremos los puntos de tangencia T de las cuatro circunferencias, por lo que sabremos sus radios y podremos dibujarlas.
3. DIBUJA CUATRO CIRCUNFERENCIAS TANGENTES A UNA CIRCUNFERENCIA DE RADIO 3.5 cm. TANGENTES ENTRE SI.

PASOS:
- Dibujamos una circunferencia de radio 3.5 cm.
- Dibujamos dos diámetros perpendiculares entre sí, dividiendo la circunferencia en cuatro partes iguales, donde situaremos los centros de las circunferencias solución.
- Para que las circunferencias sean tangentes entre sí, debemos hacer la bisectriz de uno de los cuadrantes de circunferencia, haremos que sean tangentes a esa recta, reduciendo el ejercicio a uno muy parecido al del cuadrado.
- Las circunferencioas solución O1, O2, O3 y O4, serán tangentes a la circunferencia en los puntos de corte de los diámetros con esta, y como sabemos que una recta tangente a una circunferencia en un punto es perpendicular al radio en ese punto, dibujaremos una recta (t) perpendicular al diámetro.
- Hacemos la bisectriz de t con la bisectriz del cuadrante y donde corte al diámetro obtenemos O1.
- O2, O3 y O4, estarán a la misma distancia del centro de la circunferencia (O) que O1.
- Para calcular los puntos de tangencia, lo único que tenemos que hacer es unir O1, O2, O3 Y O4.
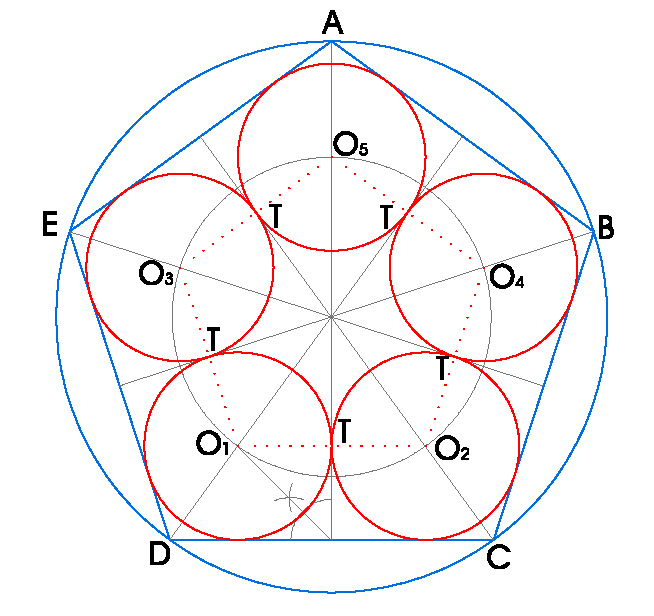
4. DIBUJA CINCO CIRCUNFERENCIAS INSCRITAS EN UN PENTÁGONO INSCRITO EN UNA CIRCUNFERENCIA DE RADIO 3.5 cm. TANGENTES ENTRE SI.

PASOS:
- Dibujamos un pentágono regular inscrito en la circunferencia de radio 3.5.
- Dibujamos sus alturas, segmentos perpendiculares al lado opuesto que pasan por los vértices del pentágono.
- Hacemos la bisectriz de una de esas alturas con el lado del pentágono obteniendo O1.
- O2, O3, O4 y O5, estarán a la misma distancia del punto de corte de las alturas, y centro de la circunferencia, que O1.
- Para calcular los puntos de tangencia, lo único que tenemos que hacer es unir O1, O2, O3, O4 Y O5.


No hay comentarios:
Publicar un comentario