POLÍGONOS DADO EL LADO. MÉTODO GENERAL. POLÍGONOS INSCRITOS EN UNA CIRCUNFERENCIA

POLÍGONOS DADO EL LADO Y MÉTODO GENERAL

TEMA: POLÍGONOS

POLÍGONOS DADO EL LADO Y MÉTODO GENERAL PARA LA CONSTRUCCIÓN DE POLÍGONOS INSCRITOS EN CIRCUNFERENCIAS

1. PENTÁGONO DADO EL LADO.

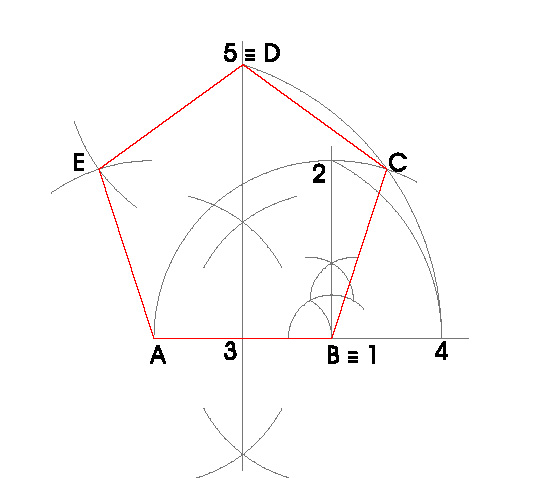
PASOS:

1. Dibujamos el segmento AB, en nuestro caso de 3 cm., que será el lado del pentágono.
2. Hacemos una perpendicular al segmento AB que pase por B.
3. Hacemos centro de compás en el punto 1 con radio 3 cm., hasta A, y donde corte a la perpendicular dibujada previamente obtenemos el punto 2.
4. Hacemos la mediatriz del segmento AB, obteniendo el punto 3.
5. Hacemos centro de compás en 3 con radio hasta el punto 2, y donde ese arco nos corte a la prolongación del segmento AB por B obtenemos el punto 4.
6. Hacemos centro de compás en A con radio hasta 4 y trazamos un arco de circunferencia, donde nos corte a la mediatriz del segmento AB obtenemos el punto 5, que será un vértice del pentágono (D).
7. Tomamos radio de compás el lado del pentágono, 3 cm., y con centro en A, B y D obtenemos E y C.
8. Una vez obtenidos los vértices del pentágono, sólo nos queda unirlos.

2. HEXÁGONO DADO EL LADO.

PASOS:

1. Dibujamos el segmento AB, que es uno de los lados del hexágono, en nuestro caso de 3 cm.
2. Hacemos centro de compás en A y en B con radio 3 cm. y donde se nos corten esos dos arcos obtenemos el punto O.
3. O será el centro de la circunferencia que circunscribirá al hexágono de lado el segmento AB.
4. Hacemos centro de compás en el punto O con radio hasta A y dibujamos la circunferencia.
5. Con radio 3 cm., marcamos en la circunferencia los demás vértices del hexágono.
6. Una vez obtenidos los vértices del hexágono, sólo nos queda unirlos.

3. HEPTÁGONO DADO EL LADO.

PASOS:

1. Dibujamos el segmento AB, que es uno de los lados del heptágono, en nuestro caso de 2,5 cm.
2. Hacemos una perpendicular al segmento AB que pase por B.
3. Hacemos la mediatriz del segmento AB.
4. Hacemos centro de compás en A con abertura hasta B y donde nos corte a la mediatriz obtenemos el punto 2.
5. Unimos A con 2, dibujando un ángulo.
6. Hacemos la bisectriz de ese ángulo.
7. Donde la bisectriz nos corte a la perpendicular a AB trazada por B, obtenemos el punto 3.
8. Hacemos centro de compás en A con abertura hasta 3, y donde ese arco nos corte a la mediatriz obtenemos el punto O.
9. O será el centro de la circunferencia que circunscribirá al heptágono de lado el segmento AB.
10. Hacemos centro de compás en el punto O con radio hasta A y dibujamos la circunferencia.
11. Con radio 2,5 cm., marcamos en la circunferencia los demás vértices del heptágono.
12. Una vez obtenidos los vértices del heptágono, sólo nos queda unirlos.

4. OCTÓGONO DADO EL LADO.

PASOS:

1. Dibujamos el segmento AB, que es uno de los lados del octógono, en nuestro caso de 2,5 cm.
2. Hacemos la mediatriz del segmento AB.
3. Haciendo centro de compás en el punto medio del segmento AB y radio hasta A o B hacemos un arco de circunferencia.
4. Donde ese arco de circunferencia nos corte a la mediatriz del segmento AB obtenemos el punto 1.
5. Haciendo centro de compás en 1 con radio hasta A dibujamos una cirunferencia.
6. Donde esa circunferencia nos corte a la mediatriz del segmento AB obtenemos el punto O.
7. O será el centro de la circunferencia que circunscribirá al octógono de lado el segmento AB.
8. Hacemos centro de compás en el punto O con radio hasta A y dibujamos la circunferencia.
9. Con radio 2,5 cm., marcamos en la circunferencia los demás vértices del octógono.
10. Una vez obtenidos los vértices del octógono, sólo nos queda unirlos.

5. MÉTODO GENERAL PARA LA CONSTRUCCIÓN DE POLÍGONOS INSCRITOS EN UNA CIRCUNFERENCIA.

Este procedimiento se utilizará solo cuando el polígono buscado no tenga una construcción particular, ni pueda obtenerse como múltiplo de otro, dado que este procedimiento lleva inherente una gran imprecisión.
Sirve para dibujar polígonos inscritos en una circunferencia de cualquier número de lados.
A mayor sea el número de lados, mayor será la imprecisión.
En nuestro caso lo vamos a utilizar para dibujar un eneágono inscrito en una circunferencia de radio 3,5 cm.

PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el eneágono, en nuestro caso de radio 3,5 cm.
2. Dibujamos sus diámetros vertical usando la escuadra y el cartabón.
3. Dividimos el diámetro en nueve partes iguales utilizando Tales.
4. Hacemos centro de compás en los dos puntos de intersección del diámetro con la circunferencia con radio el diámetro y dónde se nos corten obtenemos el punto 1.
5. Unimos el punto 1 con el punto de la segunda división del diámetro, y dónde esa semirrecta nos corte a la circunferencia obtenemos un vértice del eneágono, B.
6. Ahora ya conocemos el lado del eneágono inscrito en una circunferencia de radio 3,5 cm.
7. Con radio AB, vamos marcando el resto de los vértices del eneágono en la circunferencia.
8. Una vez obtenidos los vértices del eneágono, sólo nos queda unirlos.

TEMA: POLÍGONOS INSCRITOS EN CIRCUNFERENCIAS

Cuando un polígono tiene todos sus vértices en la circunferencia, el polígono recibe el nombre de polígono inscrito en una circunferencia.

1. PENTÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

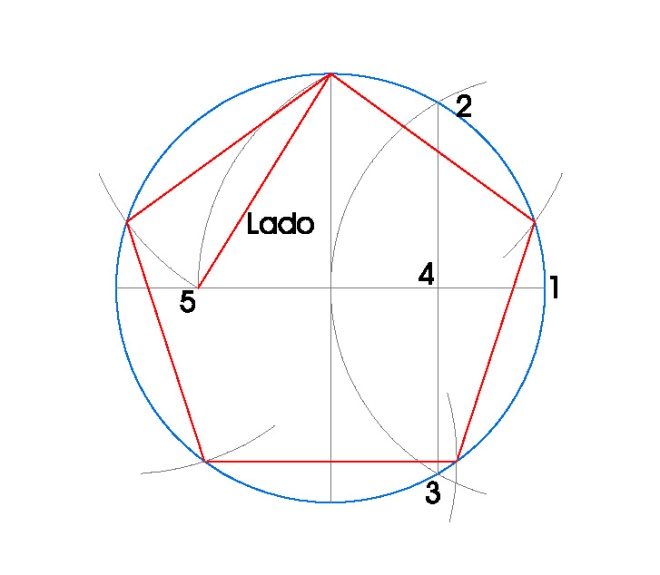
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
4. Uniendo los puntos 2 y 3 obtenemos el punto 4, que es el punto medio del radio de la circunferencia.
5. Hacemos centro de compás en 4 con radio hasta donde el diámetro vertical nos corta a la circunferencia y hacemos un arco, obteniendo 5.
6. Ya hemos obtenido el lado del pentágono inscrito.
7. Tomamos radio de compás el lado del pentágono inscrito y vamos marcando los vértices del pentágono en la circunferencia.
8. Una vez obtenidos los vértices del pentágono, sólo nos queda unirlos.

2. HEXÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

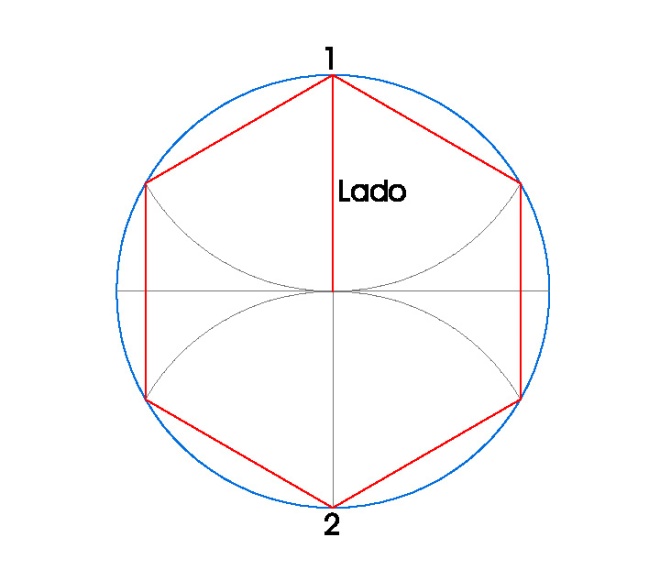
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el hexágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y donde ese arco se corta con la circunferencia obtenemos dos vértices del hexágono.
4. Hacemos centro de compás en el punto 2 con radio 3 cm. y donde ese arco se corta con la circunferencia obtenemos otros dos vértices del hexágono.
5. Los otros dos vértices del hexágono son los puntos 1 y 2.
6. Una vez obtenidos los vértices del hexágono, sólo nos queda unirlos.

3. HEPTÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

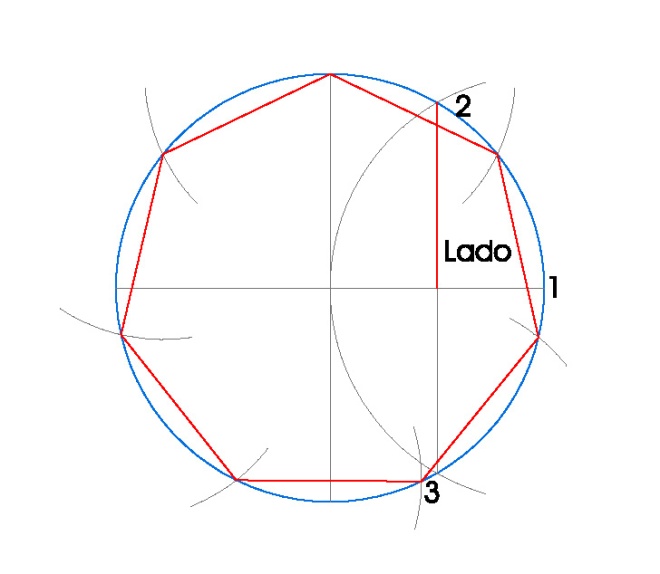
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el heptágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
4. Uniendo los puntos 2 y 3 obtenemos el lado del heptágono inscrito.
5. Tomamos radio de compás el lado del heptágono inscrito y vamos marcando los vértices del heptágono en la circunferencia.
6. Una vez obtenidos los vértices del heptágono, sólo nos queda unirlos.

4. OCTÓGONO INSCRITO EN UNA CIRCUNFERENCIA.

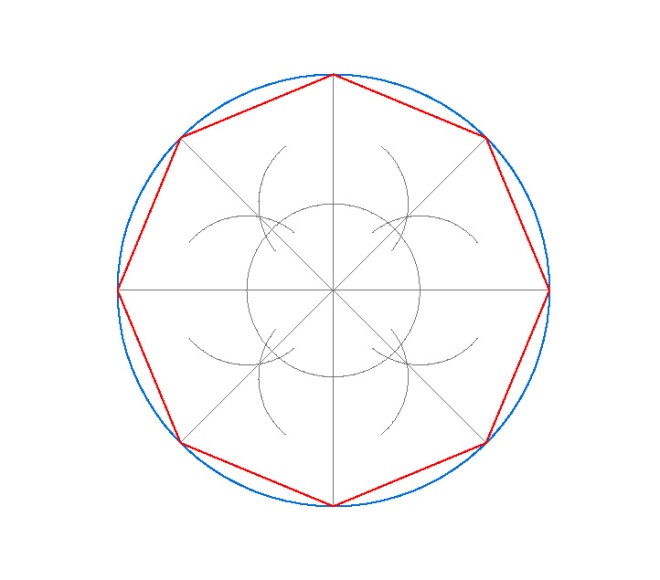
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Ya tenemos la circunferencia dividida en 4 partes.
4. Para dividirla en 8 partes, no tenemos más que hacer las bisectrices de los 4 ángulos de 90º en que está dividida la circunferencia.
5. Una vez obtenidos los vértices del octógono, sólo nos queda unirlos.

5. ENEÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

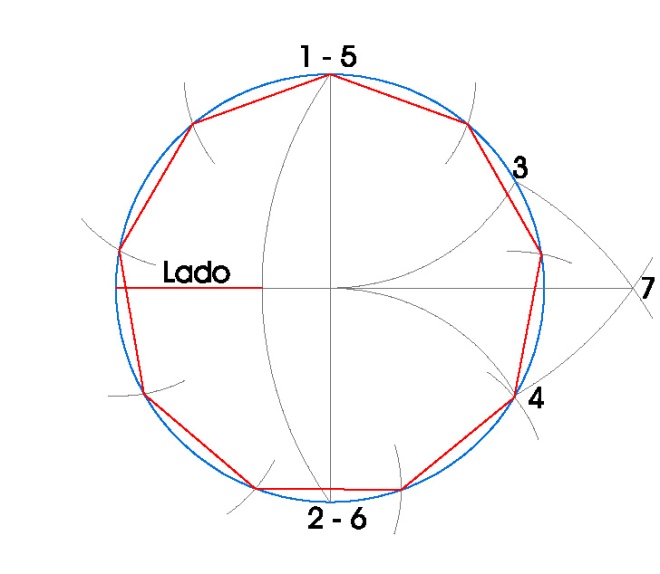
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos el punto 3.
4. Hacemos centro de compás en el punto 2 con radio 3 cm. y obtenemos el punto 4.
5. Hacemos centro de compás en el punto 5 con radio hasta el punto 4 y dibujamos un arco.
6. Hacemos centro de compás en el punto 5 con radio hasta el punto 3 y dibujamos otro arco.
7. Donde esos dos arcos se cortan obtenemos el punto 7.
8. Hacemos centro de compás en el punto 7 con radio hasta el punto 1, que coincide con el 5, y dibujamos un arco.
9. El lado del eneágono inscrito es la distancia que queda desde donde ese arco nos corta al diámetro de la circunferencia hasta la circunferencia.
10. Tomamos radio de compás el lado del eneágono inscrito y vamos marcando los vértices del eneágono en la circunferencia.
11. Una vez obtenidos los vértices del eneágono, sólo nos queda unirlos.

6. DECÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

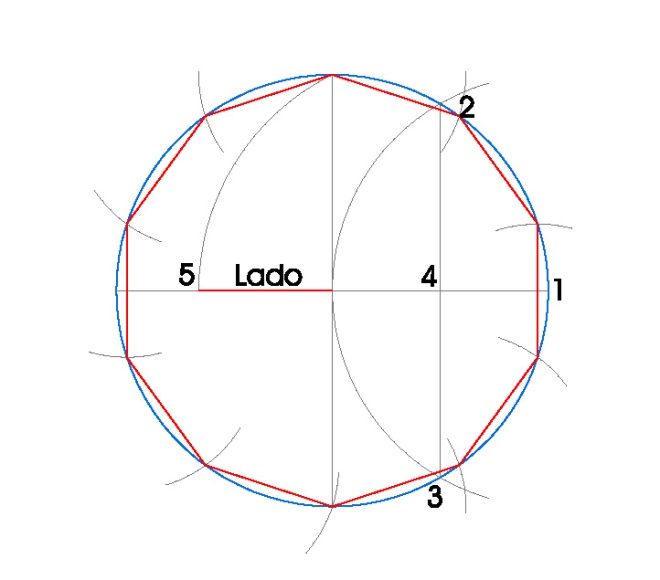
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el decágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
4. Uniendo los puntos 2 y 3 obtenemos el punto 4, que es el punto medio del radio de la circunferencia.
5. Hacemos centro de compás en 4 con radio hasta donde el diámetro vertical nos corta a la circunferencia y hacemos un arco, obteniendo 5.
6. Él lado del decágono inscrito, es la distancia desde 5 hasta el centro de la circunferencia.
7. Tomamos radio de compás el lado del decágono inscrito y vamos marcando los vértices del decágono en la circunferencia.
8. Una vez obtenidos los vértices del decágono, sólo nos queda unirlos.