CUADRILÁTEROS
Resulta un tanto difícil hacer una clasificación de los cuadriláteros, por lo que como introducción a este tema, cito textualmente la definición de cuadriláteros que hace Euclides en su libro “Los Elementos”
“Definición 22. De los cuadriláteros, cuadrado es el que tiene los lados iguales y los ángulos rectos; rectángulo el que es rectangular pero no equilátero; rombo el que es equilátero, pero no tiene los ángulos rectos; y romboide el que tiene los lados y los ángulos opuestos iguales, pero ni es equilátero ni tiene los ángulos rectos. Los otros cuadriláteros se llaman trapecios.”
Un cuadrilátero es un polígono que tiene 4 lados. Los cuadriláteros pueden tener distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales, y la suma de sus ángulos internos siempre da como resultado 360º.
Existen cuadriláteros simples y cuadriláteros complejos. Sólo vamos a estudiar los cuadriláteros simples, aquellos cuyos lados no se cortan:
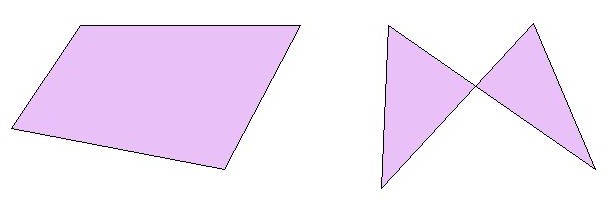

Clasificación de los cuadriláteros
Los cuadriláteros se dividen en cuadriláteros convexos y cuadriláteros cóncavos.
Un cuadrilátero es convexo, cuando ninguno de sus ángulos interiores es mayor de 90º.
Un cuadrilátero es cóncavo, cuando uno de sus ángulos interiores es mayor de 90º.
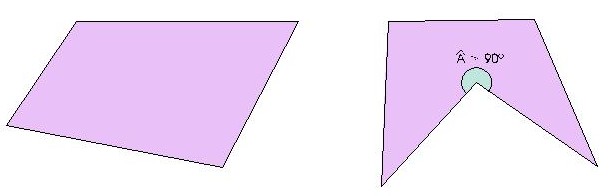
Un cuadrilátero es convexo, cuando ninguno de sus ángulos interiores es mayor de 90º.
Un cuadrilátero es cóncavo, cuando uno de sus ángulos interiores es mayor de 90º.

Cuadriláteros convexos
A. Paralelogramos
Un Paralelogramo es un cuadrilátero que tiene los lados paralelos 2 a 2. Los paralelogramos a su vez, se dividen en:
Un Paralelogramo es un cuadrilátero que tiene los lados paralelos 2 a 2. Los paralelogramos a su vez, se dividen en:
- Rectángulos: Todos sus ángulos interiores miden 90º.
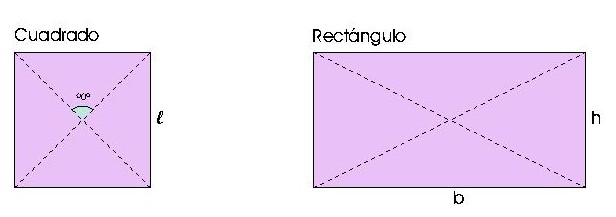
- Cuadrado: Tiene todos sus lados iguales.
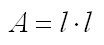
- Rectángulo: Tiene sus lados iguales dos a dos.
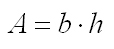
- Oblicuángulos: Tienen los ángulos interiores iguales dos a dos, los ángulos interiores opuestos son iguales, dos ángulos interiores obtusos y dos ángulos interiores agudos.
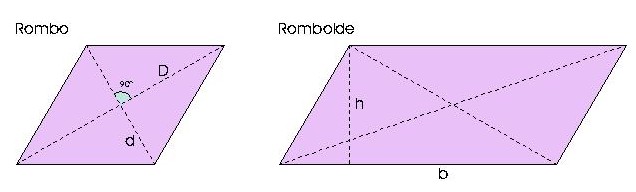
- Rombo: Tiene todos sus lados iguales.
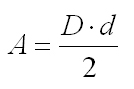
- Romboide: Tiene sus lados iguales dos a dos.
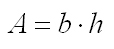
B. Trapecios
Un Trapecio es un cuadrilátero que tiene dos lados paralelos y otros dos que no lo son. Los lados paralelos se llaman bases del trapecio y la distancia entre ellos, altura.
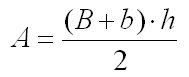
Los trapecios a su vez, se dividen, según la disposición de los lados no paralelos, en:
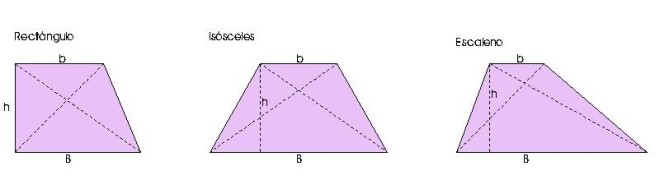
Un Trapecio es un cuadrilátero que tiene dos lados paralelos y otros dos que no lo son. Los lados paralelos se llaman bases del trapecio y la distancia entre ellos, altura.
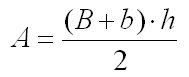
Los trapecios a su vez, se dividen, según la disposición de los lados no paralelos, en:

- Rectángulos: Tienen uno de los lados no paralelos perpendicular a los dos lados paralelos.
- Isósceles: Tienen iguales los dos lados no paralelos.
- Escalenos: Tienen distintos los dos lados no paralelos.
C. Trapezoides
Un Trapezoide es un cuadrilátero que no tiene lados paralelos entre sí.
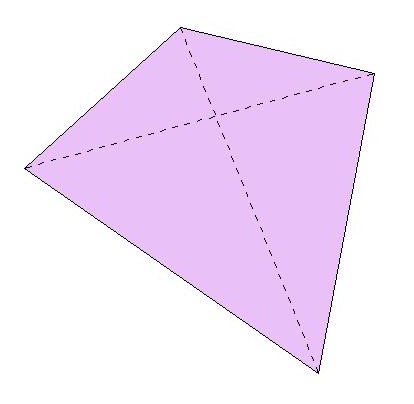
Un Trapezoide es un cuadrilátero que no tiene lados paralelos entre sí.

EJERCICIOS
1. ROMBO DE LADO l = 5,5 cm Y UNO DE SUS ÁNGULOS ENTRE LADOS 75º.
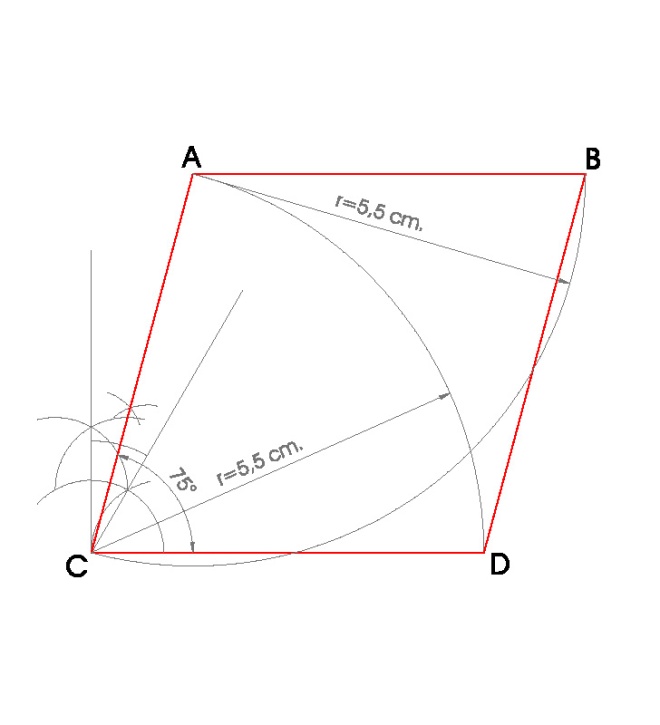
PASOS:
- Dibujamos el lado dado l = 5,5 cm. y llamamos a sus extremos C y D, son dos vértices del rombo.
- Hacemos la perpendicular a el segmento por el punto C, para trazar un ángulo de 75º con vértice en C.
- Trazamos un arco de circunferencia con centro en C y radio el lado l = 5,5 cm.
- Donde el arco de circunferencia nos corte al ángulo de 75º obtenemos otro vértice del rombo A .
- Trazamos un arco de circunferencia con centro en D y radio el lado l = 5,5 cm.
- Trazamos un arco de circunferencia con centro en A y radio el lado l = 5,5 cm.
- Donde esos dos arcos se corten obtenemos el último vértice del rombo B.
- Uniendo A, B, C y D obtengo el rombo.
2. ROMBOIDE DE LADO MAYOR L = 5,5 cm., LADO MENOR l = 4,5 cm. Y UNO DE SUS ÁNGULOS ENTRE LADOS 75º.
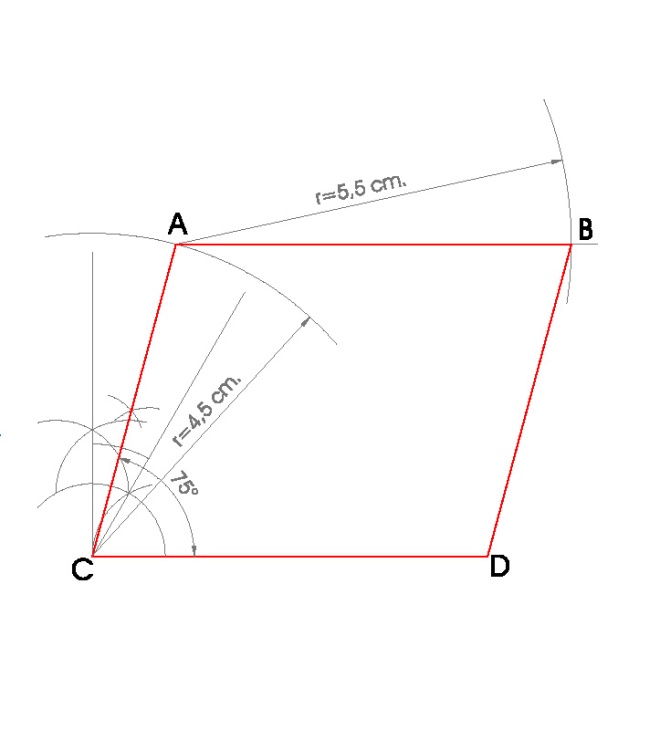
PASOS:
- Dibujamos el lado mayor L = 5,5 cm. y llamamos a sus extremos C y D, son dos vértices del romboide.
- Hacemos la perpendicular a el segmento por el punto C, para trazar un ángulo de 75º con vértice en C.
- Trazamos un arco de circunferencia con centro en C y radio el lado menor l = 4,5 cm.
- Donde el arco de circunferencia nos corte al ángulo de 75º obtenemos otro vértice del rombo A .
- Trazamos un arco de circunferencia con centro en A y radio el lado mayor L = 5,5 cm.
- Trazamos un arco de circunferencia con centro en D y radio el lado menor l = 4,5 cm.
- Donde esos dos arcos se corten obtenemos el último vértice del romboide B.
- Uniendo A, B, C y D obtengo el romboide.
3. TRAPECIO ISÓSCELES DE BASE MAYOR B = 6,5 cm., BASE MENOR b = 4 cm. Y ALTURA h = 3,5 cm.
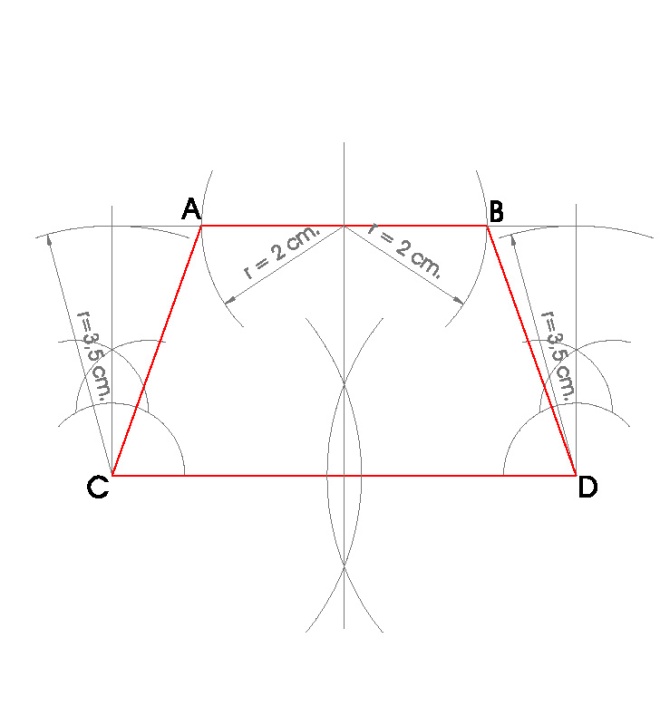
PASOS:
- Dibujamos la base mayor del trapecio B = 6,5 cm. y llamamos a sus extremos C y D, son dos vértices del trapecio.
- Hacemos la perpendicular a el segmento por el punto C y hacemos lo mismo en el punto D.
- Trazamos un arco de circunferencia con centro en C y radio la altura h = 3,5 cm. y hacemos lo mismo en D
- Uniendo los puntos donde esos dos arcos nos corten a las perpendiculares hacemos la paralela al lado CD
- Hacemos la mediatriz del lado CD
- Desde donde la mediatriz nos corte a la paralela realizada previamente, hacemos dos arcos de circunferencia con radio la mitad de la base menor del trapecio b/2 = 2 cm.
- Donde esos dos arcos nos corten a la paralela obtenemos los vértices A y B del trapecio.
- Uniendo A, B, C y D obtengo el trapecio isósceles.
4. TRAPECIO RECTÁNGULO DE BASE MAYOR B = 6,5 cm., BASE MENOR b = 3,5 cm. Y DIAGONAL MAYOR D = 7,5 cm.
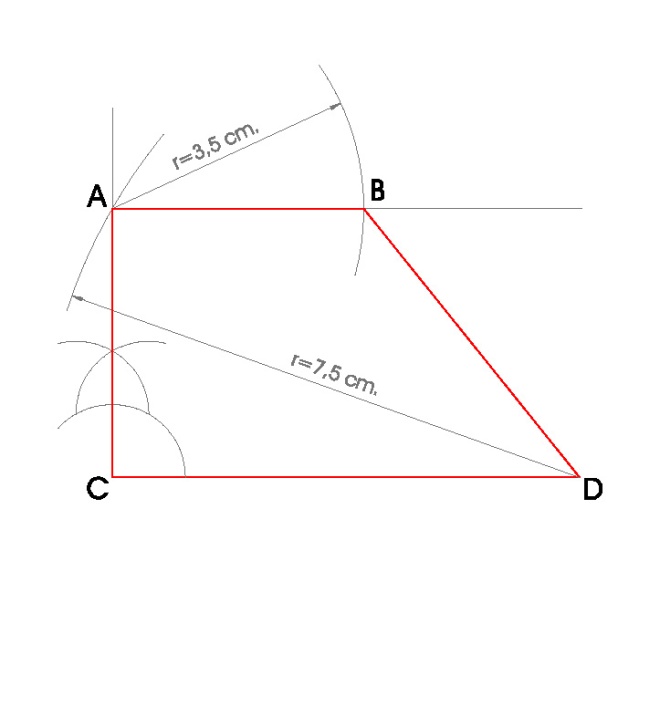
- Dibujo la base mayor B = 6,5 cm. y llamo a sus extremos C y D, son dos vértices del trapecio.
- Hacemos la mediatriz al segmento por el vértice C.
- Hago un arco de circunferencia con centro en D y radio la diagonal mayor D = 7,5 cm.
- Donde ese arco de circunferencia nos corte a la perpendicular obtengo el vértice del trapecio A.
- Hago una paralela al segmento CD por el punto A.
- Hago un arco de compás con centro en A y radio la base menor del trapecio b = 3,5 cm.
- Donde ese arco nos corte a la paralela obtengo el último vértice del trapecio B.
- Uniendo A, B, C y D obtengo el trapecio rectángulo.
5. CUADRADO DE LADO l = 5 cm.
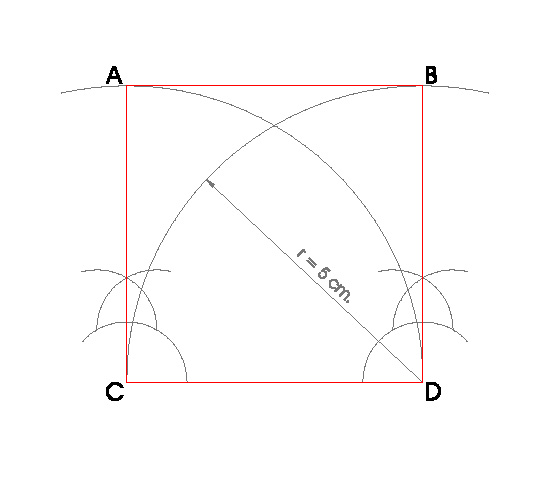
PASOS:
- Dibujamos el lado dado l = 5 cm. y llamamos a sus extremos C y D, son dos vértices del cuadrado.
- Hacemos la perpendicular a el segmento por el punto C y hacemos lo mismo en el punto D.
- Trazamos un arco de circunferencia con centro en C y radio el lado l = 5 cm.
- Donde el arco de circunferencia nos corte a la perpendicular por el punto C obtenemos el punto A .
- Hacemos lo mismo en el punto D y donde el arco nos corte a la perpendicular obtenemos el punto B.
- Uniendo A, B, C y D obtengo el cuadrado.
6. CUADRADO DE DIAGONAL d = 5,5 cm.
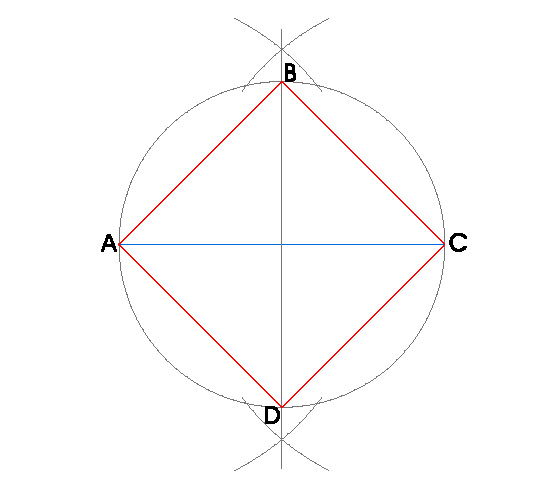
PASOS:
- Dibujamos la diagonal dada y llamamos a sus extremos A y C, son dos vértices del cuadrado.
- Hacemos la mediatriz del segmento AC.
- Obtenido el punto medio del segmento AC, hacemos una circunferencia con centro en ese punto y radio hasta uno de los extremos del segmento, A o C.
- Donde la circunferencia nos corte a la mediatriz, obtenemos los otros dos vértices del cuadrado B y D.
- Uniendo A, B, C y D obtengo el cuadrado.
7. RECTÁNGULO DE LADO MAYOR L = 5 cm. Y LADO MENOR l = 3,5 cm.
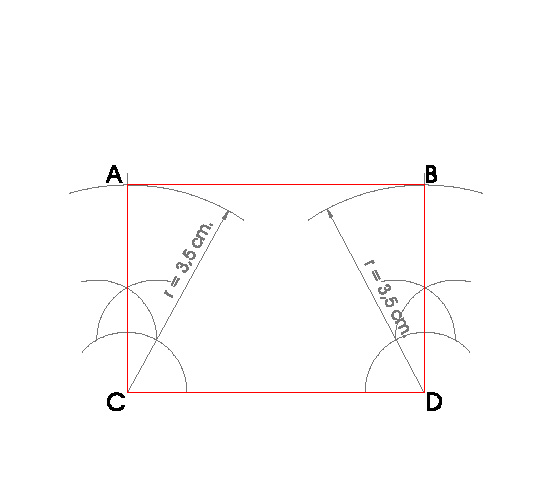
PASOS:
- Dibujamos el lado mayor del rectángulo L = 5 cm. y llamamos a sus extremos C y D, son dos vértices del rectángulo.
- Hacemos la perpendicular a el segmento por el punto C y hacemos lo mismo en el punto D.
- Trazamos un arco de circunferencia con centro en C y radio el lado menor l = 3,5 cm.
- Hacemos lo mismo en el punto D
- Donde esos dos arcos nos corten a las perpendiculares obtenemos los otros dos vértices del rectángulo A y B
- Uniendo A, B, C y D obtengo el rectángulo.
8. RECTÁNGULO DE DIAGONAL d = 6,5 cm. Y LADO MENOR l = 3 cm.
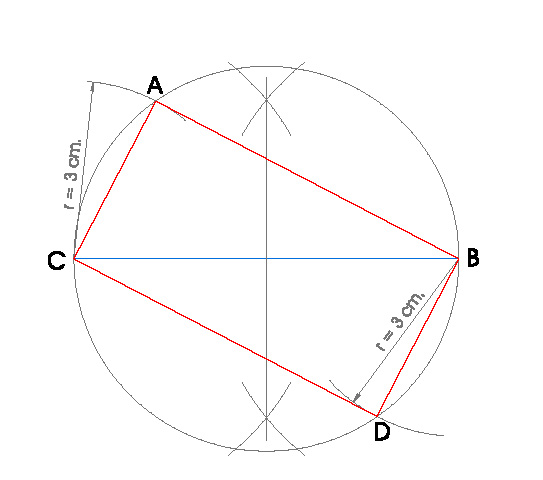
PASOS:
- Dibujo la diagonal dada d = 6,5 cm. y llamo a sus extremos C y B, son dos vértices del rectángulo
- Hacemos la mediatriz del segmento CB.
- Obtenido el punto medio del segmento CB, hacemos una circunferencia con centro en ese punto y radio hasta uno de los extremos del segmento, C o B.
- Hacemos un arco de circunferencia de radio el lado menor del rectángulo l = 3 cm. y centro en C y B
- Donde los arcos nos corten a la circunferencia obtenemos los otros dos vértices del rectángulo A y D.
- Uniendo A, B, C y D obtengo el rectángulo.
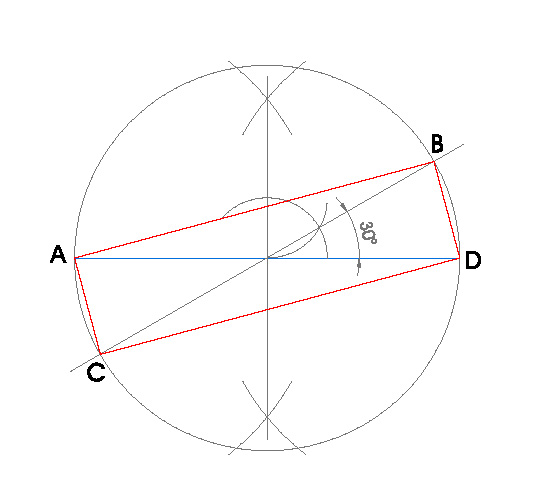
9. RECTÁNGULO DE DIAGONAL d = 6,5 cm. Y ÁNGULO ENTRE DIAGONALES 30º
PASOS:
- Dibujo la diagonal de 6,5 cm. y llamo a sus extremos A y D, son dos vértices del rectángulo.
- Hacemos la mediatriz del segmento AD.
- Obtenido el punto medio del segmento AD, hacemos una circunferencia con centro en ese punto y radio hasta uno de los extremos del segmento, A o D.
- Después dibujo un ángulo de 30º en el punto medio de la diagonal.
- Donde el ángulo nos corte a la circunferencia obtenemos los otros dos vértices del rectángulo B y C.
- Uniendo A, B, C y D obtengo el rectángulo.
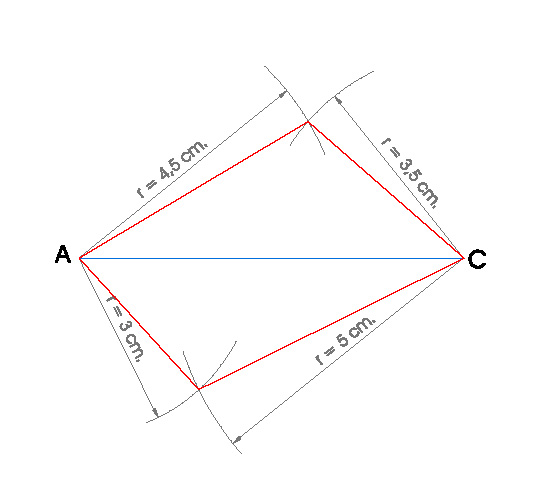
10. CUADRILÁTERO, DADOS LOS LADOS Y UNA DIAGONAL AB = 4,5 cm., BC = 3,5 cm., CD = 5 cm., DA = 3 cm., AC = 6,5 CM.
PASOS:
- Dibujo la diagonal AC.
- Hago un arco con centro en A y radio AB = 4,5 cm.
- Hago un arco con centro en C y radio BC = 3,5 cm.
- Donde se cortan esos dos arcos obtengo el vértice B del cuadrilátero.
- Hago un arco con centro en A y radio el lado DA = 3 cm.
- Hago un arco con centro en C y radio el lado CD = 5 cm..
- Donde se cortan esos dos arcos obtengo el vértice D del cuadrilátero.
- Uniendo A, B, C y D obtengo el cuadrilátero.


No hay comentarios:
Publicar un comentario