TEMA: POLÍGONOS
ELEMENTOS FUNDAMENTALES

- Lado: Es cualquiera de los segmentos que conforman la línea poligonal que delimita el polígono.
- Vértice: Es el punto donde se unen dos lados consecutivos. El número de vértices coincide con el número de lados del polígono.
- Diagonal: Es cada uno de los segmentos que une dos vértices no consecutivos.
El número de diagonales que se pueden trazar desde un vértice en un polígono de n lados es:
 Si desde cada vértice se pueden trazar esas diagonales, el número total de diagonales que se pueden trazar en un polígono será por tanto:
Si desde cada vértice se pueden trazar esas diagonales, el número total de diagonales que se pueden trazar en un polígono será por tanto:
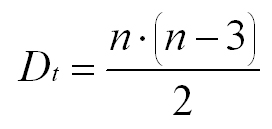
- Ángulo interior: Es el formado por dos lados consecutivos.
Las diagonales trazadas desde un vértice, dividen al polígono en triángulos. Ya sabemos que la suma de los ángulos interiores de un triángulo es 180º, por lo tanto la suma de los ángulos interiores de un polígono será:

- Ángulo exterior: Es el formado por un lado y la prolongación de otro consecutivo.
Si nos fijamos en la figura, un ángulo exterior y su interior contiguo son adyacentes, esto es, sonconsecutivos y además suman 180º:
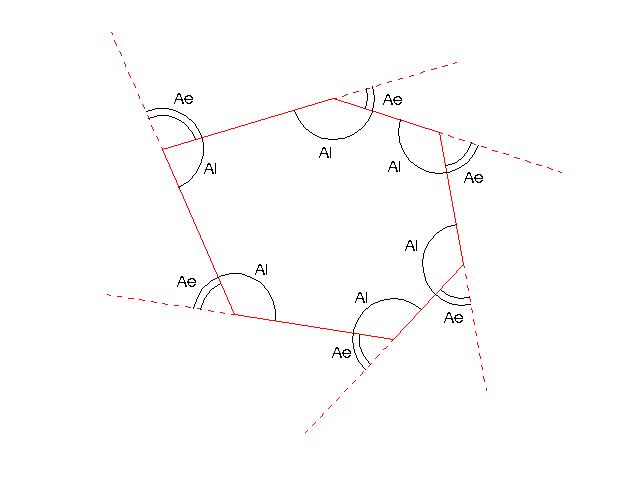 De este modo, sabemos que la suma del total de los ángulos interiores y exteriores de un polígono es n x 180º, así que la suma total de los ángulos exteriores de un polígono será:
De este modo, sabemos que la suma del total de los ángulos interiores y exteriores de un polígono es n x 180º, así que la suma total de los ángulos exteriores de un polígono será:


Un polígono es la porción del plano delimitada por una línea poligonal cerrada. Sus principales elementos son:

- Lado: Es cualquiera de los segmentos que conforman la línea poligonal que delimita el polígono.
- Vértice: Es el punto donde se unen dos lados consecutivos. El número de vértices coincide con el número de lados del polígono.
- Diagonal: Es cada uno de los segmentos que une dos vértices no consecutivos.
El número de diagonales que se pueden trazar desde un vértice en un polígono de n lados es:

Si desde cada vértice se pueden trazar esas diagonales, el número total de diagonales que se pueden trazar en un polígono será por tanto:
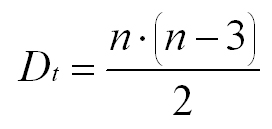
- Ángulo interior: Es el formado por dos lados consecutivos.
Las diagonales trazadas desde un vértice, dividen al polígono en triángulos. Ya sabemos que la suma de los ángulos interiores de un triángulo es 180º, por lo tanto la suma de los ángulos interiores de un polígono será:

- Ángulo exterior: Es el formado por un lado y la prolongación de otro consecutivo.
Si nos fijamos en la figura, un ángulo exterior y su interior contiguo son adyacentes, esto es, sonconsecutivos y además suman 180º:

De este modo, sabemos que la suma del total de los ángulos interiores y exteriores de un polígono es n x 180º, así que la suma total de los ángulos exteriores de un polígono será:


1. CLASIFICACIÓN DE LOS POLÍGONOS.
1.1. SEGÚN EL NÚMERO DE LADOS.
Número de lados Nombre del polígono 3 Triángulo 4 Cuadrilátero 5 Pentágono 6 Hexágono 7 Heptágono 8 Octágono 9 Eneágono o Nonágono 10 Decágono 11 Endecágono 12 Dodecágono 13 Tridecágono 14 Tetradecágono 15 Pentadecágono 16 Hexadecágono 17 Heptadecágono 18 Octadecágono 19 Eneadecágono
Para saber cómo se llama un polígono de menos de cien lados podemos hacer lo siguiente. Primero contamos el número de lados que tiene, hacemos una combinación de prefijos como se muestra a continuación y agregamos la terminación gono.
Decenas y Unidades Terminación -kai- 1 -hená- -gono 20 Icosa- 2 -dí- 30 Triaconta- 3 -trí- 40 Tetraconta- 4 -tetrá- 50 Pentaconta- 5 -pentá- 60 Hexaconta- 6 -hexá- 70 Heptaconta- 7 -heptá- 80 Octaconta- 8 -octá- 90 Eneaconta- 9 -eneá-
POLÍGONOS INSCRITOS EN CIRCUNFERENCIAS
| Número de lados | Nombre del polígono |
| 3 | Triángulo |
| 4 | Cuadrilátero |
| 5 | Pentágono |
| 6 | Hexágono |
| 7 | Heptágono |
| 8 | Octágono |
| 9 | Eneágono o Nonágono |
| 10 | Decágono |
| 11 | Endecágono |
| 12 | Dodecágono |
| 13 | Tridecágono |
| 14 | Tetradecágono |
| 15 | Pentadecágono |
| 16 | Hexadecágono |
| 17 | Heptadecágono |
| 18 | Octadecágono |
| 19 | Eneadecágono |
Para saber cómo se llama un polígono de menos de cien lados podemos hacer lo siguiente. Primero contamos el número de lados que tiene, hacemos una combinación de prefijos como se muestra a continuación y agregamos la terminación gono.
| Decenas | y | Unidades | Terminación | ||
| -kai- | 1 | -hená- | -gono | ||
| 20 | Icosa- | 2 | -dí- | ||
| 30 | Triaconta- | 3 | -trí- | ||
| 40 | Tetraconta- | 4 | -tetrá- | ||
| 50 | Pentaconta- | 5 | -pentá- | ||
| 60 | Hexaconta- | 6 | -hexá- | ||
| 70 | Heptaconta- | 7 | -heptá- | ||
| 80 | Octaconta- | 8 | -octá- | ||
| 90 | Eneaconta- | 9 | -eneá- | ||
POLÍGONOS INSCRITOS EN CIRCUNFERENCIAS
Cuando un polígono tiene todos sus vértices en la circunferencia, el polígono recibe el nombre de polígono inscrito en una circunferencia.
1. PENTÁGONO INSCRITO EN UNA CIRCUNFERENCIA.
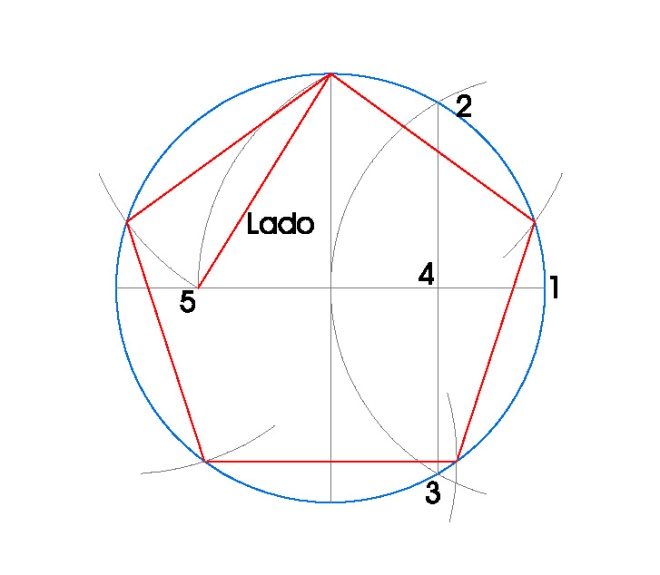
PASOS:
- Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
- Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
- Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
- Uniendo los puntos 2 y 3 obtenemos el punto 4, que es el punto medio del radio de la circunferencia.
- Hacemos centro de compás en 4 con radio hasta donde el diámetro vertical nos corta a la circunferencia y hacemos un arco, obteniendo 5.
- Ya hemos obtenido el lado del pentágono inscrito.
- Tomamos radio de compás el lado del pentágono inscrito y vamos marcando los vértices del pentágono en la circunferencia.
- Una vez obtenidos los vértices del pentágono, sólo nos queda unirlos.
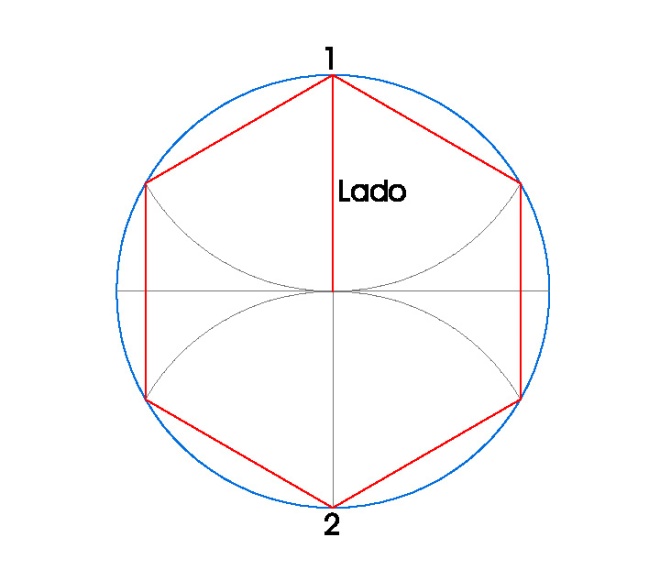
2. HEXÁGONO INSCRITO EN UNA CIRCUNFERENCIA.
PASOS:
- Dibujamos la circunferencia en la que vamos a inscribir el hexágono, en nuestro caso de radio 3 cm.
- Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
- Hacemos centro de compás en el punto 1 con radio 3 cm. y donde ese arco se corta con la circunferencia obtenemos dos vértices del hexágono.
- Hacemos centro de compás en el punto 2 con radio 3 cm. y donde ese arco se corta con la circunferencia obtenemos otros dos vértices del hexágono.
- Los otros dos vértices del hexágono son los puntos 1 y 2.
- Una vez obtenidos los vértices del hexágono, sólo nos queda unirlos.
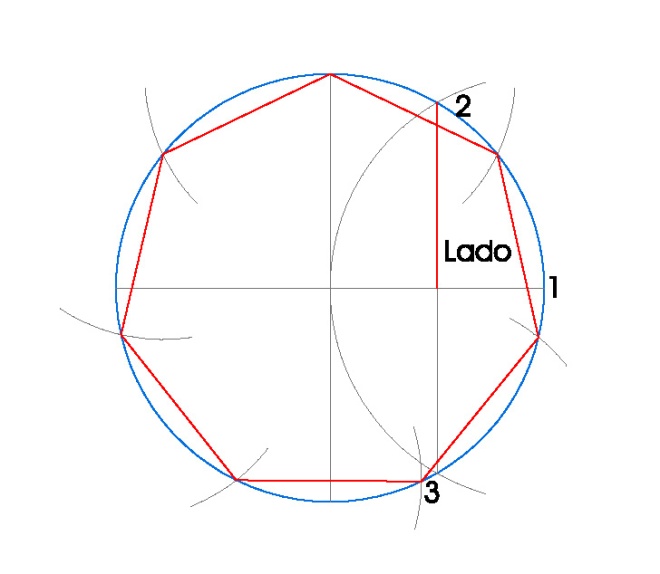
3. HEPTÁGONO INSCRITO EN UNA CIRCUNFERENCIA.
PASOS:
- Dibujamos la circunferencia en la que vamos a inscribir el heptágono, en nuestro caso de radio 3 cm.
- Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
- Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
- Uniendo los puntos 2 y 3 obtenemos el lado del heptágono inscrito.
- Tomamos radio de compás el lado del heptágono inscrito y vamos marcando los vértices del heptágono en la circunferencia.
- Una vez obtenidos los vértices del heptágono, sólo nos queda unirlos.
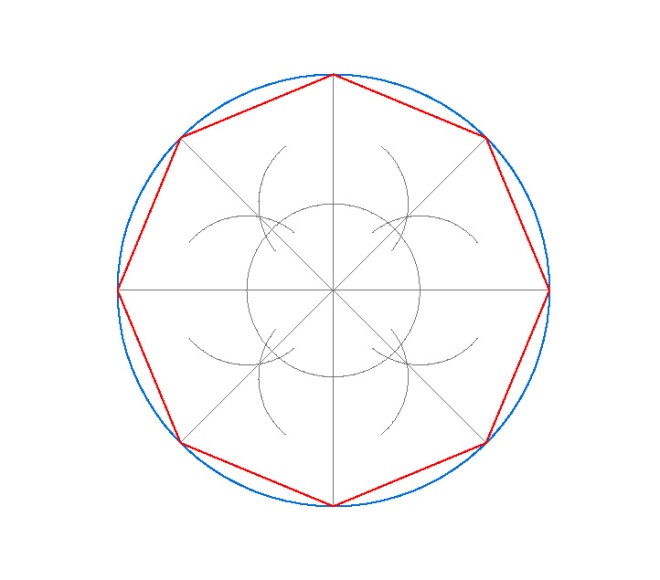
4. OCTÓGONO INSCRITO EN UNA CIRCUNFERENCIA.
PASOS:
- Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
- Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
- Ya tenemos la circunferencia dividida en 4 partes.
- Para dividirla en 8 partes, no tenemos más que hacer las bisectrices de los 4 ángulos de 90º en que está dividida la circunferencia.
- Una vez obtenidos los vértices del octógono, sólo nos queda unirlos.
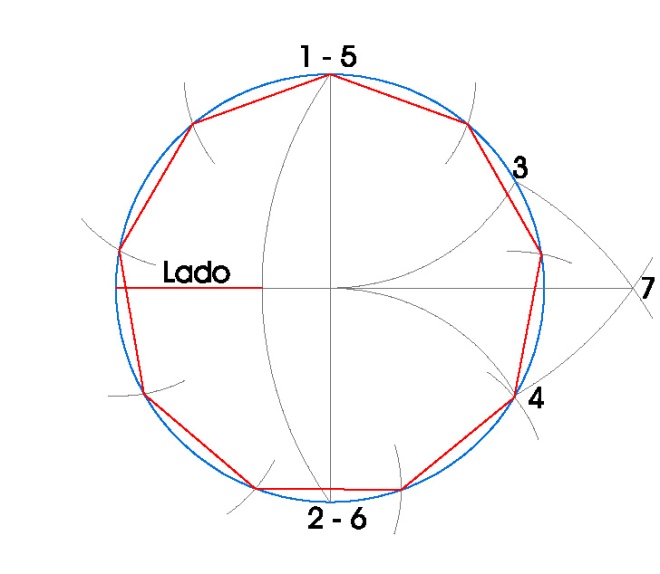
5. ENEÁGONO INSCRITO EN UNA CIRCUNFERENCIA.
PASOS:
- Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
- Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
- Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos el punto 3.
- Hacemos centro de compás en el punto 2 con radio 3 cm. y obtenemos el punto 4.
- Hacemos centro de compás en el punto 5 con radio hasta el punto 4 y dibujamos un arco.
- Hacemos centro de compás en el punto 5 con radio hasta el punto 3 y dibujamos otro arco.
- Donde esos dos arcos se cortan obtenemos el punto 7.
- Hacemos centro de compás en el punto 7 con radio hasta el punto 1, que coincide con el 5, y dibujamos un arco.
- El lado del eneágono inscrito es la distancia que queda desde donde ese arco nos corta al diámetro de la circunferencia hasta la circunferencia.
- Tomamos radio de compás el lado del eneágono inscrito y vamos marcando los vértices del eneágono en la circunferencia.
- Una vez obtenidos los vértices del eneágono, sólo nos queda unirlos.
6. DECÁGONO INSCRITO EN UNA CIRCUNFERENCIA.
PASOS:
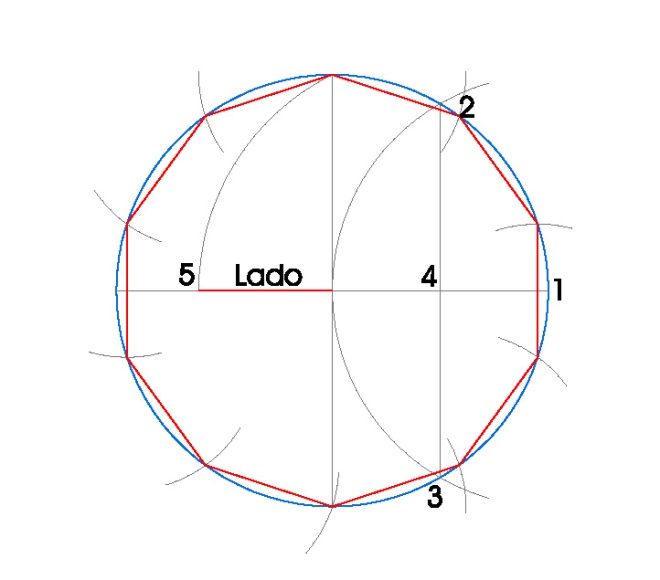
- Dibujamos la circunferencia en la que vamos a inscribir el decágono, en nuestro caso de radio 3 cm.
- Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
- Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
- Uniendo los puntos 2 y 3 obtenemos el punto 4, que es el punto medio del radio de la circunferencia.
- Hacemos centro de compás en 4 con radio hasta donde el diámetro vertical nos corta a la circunferencia y hacemos un arco, obteniendo 5.
- Él lado del decágono inscrito, es la distancia desde 5 hasta el centro de la circunferencia.
- Tomamos radio de compás el lado del decágono inscrito y vamos marcando los vértices del decágono en la circunferencia.
- Una vez obtenidos los vértices del decágono, sólo nos queda unirlos.


No hay comentarios:
Publicar un comentario