reglaycompas.htm

CONSTRUCCIONES GEOMÉTRICAS

1. MEDIATRIZ DE UN SEGMENTO

Es el lugar geométrico de los puntos del plano que equidistan de los extremos de un segmento. Por lo tanto es el lugar geométrico de todos los centros de las circunferencias que pasan por dichos extremos.

PASOS:

Hacemos centro de compás en A con radio mayor que la mitad de AB.
Trazamos dos arcos de circunferencia.
Hacemos centro de compás en B con el mismo radio.
Trazamos dos arcos de circunferencia.
Donde corten a los trazados previamente obtenemos los puntos 1 y 2.
Uniendo 1 y 2 obtenemos la mediatriz del segmento AB.

2. RECTA PERPENDICULAR A OTRA POR UN PUNTO SITUADO EN ELLA

Una recta es perpendicular a otra cuando forma con ella un ángulo recto (90º)

PASOS:

Teniendo la recta (r) y un punto situado en ella (A)
Trazamos un arco de circunferencia tomando como centro A.
Ese arco de circunferencia cortará a la recta (r) en dos puntos 1 y 2.
Trazamos la mediatriz del segmento marcado en la recta (r) 12.
Uniendo los puntos 3 y 4 obtenemos la recta perpendicular a (r) que pasa por el punto A.

3. RECTA PERPENDICULAR A OTRA POR UN PUNTO EXTERIOR

Una recta es perpendicular a otra cuando forma con ella un ángulo recto (90º)

PASOS:

Teniendo la recta (r) y un punto exterior a ella (A)
Trazamos un arco de circunferencia tomando como centro A.
Ese arco de circunferencia cortará a la recta (r) en dos puntos 1 y 2.
Trazamos la mediatriz del segmento marcado en la recta (r) 12.
Uniendo los puntos 3 y 4 obtenemos la recta perpendicular a (r) que pasa por el punto A.

4. RECTA PERPENDICULAR A OTRA POR UNO DE SUS EXTREMOS

Una recta es perpendicular a otra cuando forma con ella un ángulo recto (90º)

PASOS:

Hacemos centro de compás en el punto dado A.
Trazamos un arco de circunferencia y donde corte a la recta obtenemos 1
Haciendo centro de compás en 1 con la misma abertura obtenemos 2.
Haciendo centro de compás en 2 con la misma abertura obtenemos 3.
Hacemos centro de compás en 2 y en 3 con la misma abertura y obtenemos 4.
Unimos 4 con A y obtenemos la recta perpendicular a la dada que pasa por uno de sus extremos.

5. RECTA PARALELA A OTRA POR UN PUNTO EXTERIOR – MÉTODO I

Una recta es paralela a otra cuando nunca se corta con esta.

PASOS:

Tomando centro de compás en un punto cualquiera de la recta dada (r) al que llamamos O trazamos un arco de circunferencia que pase por el punto dado A
Ese arco de circunferencia cortará a la recta (r) en dos puntos P y Q
Hacemos arco de circunferencia en P, tomando como radio la distancia QA
Donde corte al primer arco de circunferencia trazado obtenemos B
Uniendo B con A obtenemos la recta paralela a r que pasa por A.

6. RECTA PARALELA A OTRA POR UN PUNTO EXTERIOR – MÉTODO II

Una recta es paralela a otra cuando nunca se corta con esta.

PASOS:

Tomamos dos puntos aleatorios de la recta dada (r) y los llamamos P y Q
Hacemos centro en A con radio de circunferencia PQ y dibujamos la circunferencia.
Hacemos centro en Q con radio de circunferencia PA y donde corte a la primera circunferencia obtenemos B
Uniendo B con A obtenemos la recta paralela a la recta dada que pasa por A.

7. Teorema de Tales:

Si dos líneas coplanarias (que están en el mismo plano) son cortadas por un haz de rectas paralelasentre sí y también coplanarias, los segmentos determinados en ambas rectas son proporcionales.
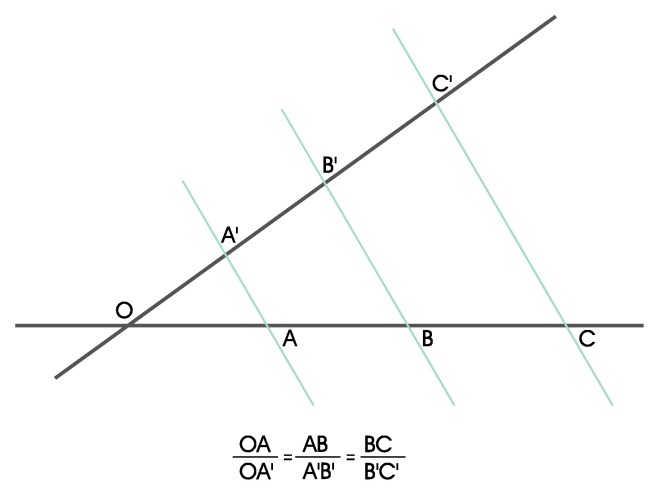
THALES-THEOREM

Usamos el teorema de Tales para dividir segmentos en partes iguales o proporcionales.

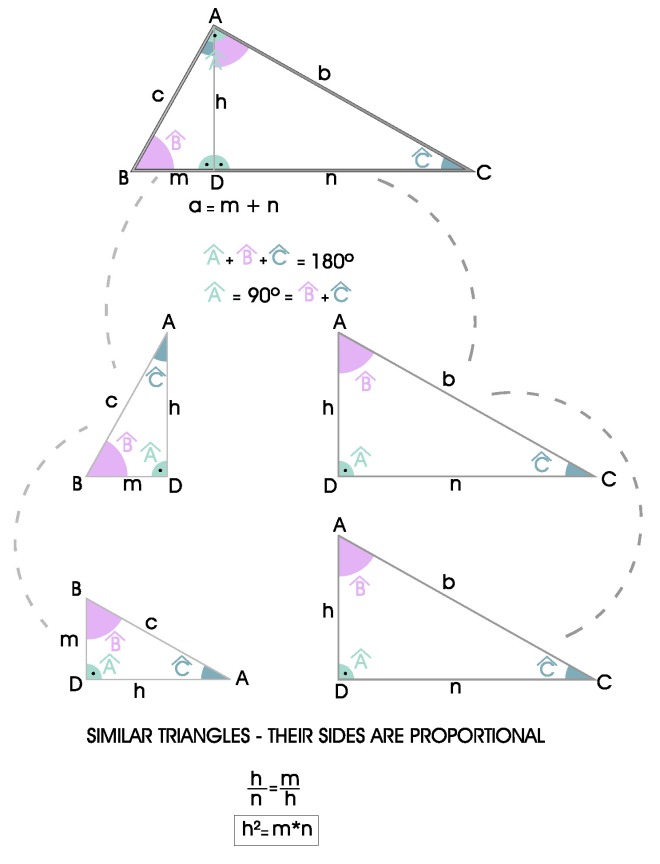
8. Teorema de la altura:

En Geometría, decimos que dos figuras son “semejantes” cuando sus ángulos son iguales y, por lo tanto, sus lados son proporcionales entre sí.
El teorema de la altura describe la relación entre la altura sobre la hipotenusa y los dos segmentosen que ésta queda dividida por dicha altura. En un triángulo rectángulo la altura sobre la hipotenusa esmedia proporcional entre los dos segmentos en que la hipotenusa queda dividida por dicha altura.
SIMILAR-TRIANGLES

9. Proporción áurea:

Aquí podéis ver un documental muy interesante acerca de la importancia de la proporción áurea:

De forma simple, la Proporción Aurea establece que lo pequeño es a lo grande como lo grande es al todo. Habitualmente esto se aplica a las proporciones entre segmentos. Dos cantidades están enProporción Áurea si su relación es la misma que la relación de su suma a la mayor de las dos cantidades. El número de oro es un número irracional que se representa mediante la letra griega $\varphi$ en honor del escultor griego Phidias.

Su expresión algebráica, para cantidades a y b, siendo a > b

Golden ratio

Donde la letra griega phi ( $\varphi$ ) representa la proporción áurea. Su valor es:

En éste tema vamos a aprender a obtenerla gráficamente:

Para saber más….

Tales de Mileto

Thales de Mileto (630 a.c al 545 a.c.) (También se puede escribir Tales de Mileto) fue un matemático griego considerado también como el primer filósofo occidental.

Fue el primero de los Siete Sabios de Grecia y uno de los grandes matemáticos de su época. Una de estas aportaciones a la geometría es el llamado “Teorema de Thales“.

Lenguaje y notación en Geometría básica

PUNTO (A, B, C,…)

Un punto es una posición exacta en el plano. Es importante entender que un punto no es una cosa, sino un lugar. Un punto no tiene dimensión.

LÍNEA (r, s, t, p…)

Se define como un punto en movimiento o la unión entre dos puntos. La líneas no tienen ni principio ni final.

SEMIRRECTA (r, s, t, p…)

Una semirrecta tiene principio pero no final.

SEGMENTO (AB, BC;…)

Es una parte de una línea. Tiene principio y final (extremos del segmento). Podemos medir la lungitud de los segmentos.

Las construcciones geométricas de longitudes, ángulos y otras figuras utilizando únicamente regla y compás son muy importantes para que luego seamos capaces de realizar construcciones más complejas.

Lugar geométrico

Lugar geométrico: Es el conjunto de todos los puntos del plano que cumplen con una condición dada. Es decir, todo lugar geométrico presenta las siguientes características: