TEMA: ÁNGULOS

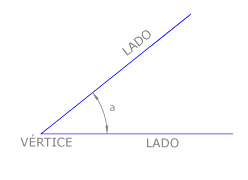
Un ángulo es la parte del plano limitada por dos semirrectas que parten del mismo punto, que es el vértice del ángulo. Las semirrectas que lo limitan son los lados del ángulo.

Nomenclatura de los ángulos

Cuando un ángulo es menor de 90º se llama agudo, si es mayor de 90º se llama obtuso y si mide 90ºse llama recto. El ángulo llano o extendido mide 180º, el ángulo completo 360º y el ángulo nulo 0º.

En el siguiente enlace http://docentes.educacion.navarra.es/msadaall/geogebra/angulos.htm podemos aprender cómo se miden ángulos:

	En una circunferencia			En una semicircunferencia
	En un triángulo: Figura 1 Figura 2 Figura 3			En un pentágono: Figura 1 Figura 2
	En un cuadrilátero			En un hexágono y un polígono cualquiera: Figura 1 Figura 2

1. TRASLACIÓN DE UN ÁNGULO

Si queremos dibujar un ángulo igual a uno dado con vértice en un punto dado A

PASOS:

Dibujamos una semirrecta desde A.
Dibujamos un arco de radio arbitrario con centro en el vértice del ángulo dado y otro arco igual con centro en A.
Ese arco nos cortará a la semirrecta en un punto.
Medimos con el compás el arco limitado por los lados del ángulo dado y llevamos tal medida con el compás sobre el arco de centro en A, desde el punto en que nos cortaba a la semirrecta.

2. BISECTRIZ DE UN ÁNGULO

Es el lugar geométrico de los puntos del plano que equidistan de los lados de un ángulo.

PASOS:

Dadas dos rectas que se cortan en un punto O.
Hacemos centro de compás en O, con la abertura que queramos y determinamos los puntos 1 y 2.
Haciendo centro de compás en 1 y 2 con abertura mayor de la mitad de su distancia obtenemos el punto 3.
Uniendo 3 con O obtenemos la recta bisectriz del ángulo.

3. BISECTRIZ DE UN ÁNGULO CUANDO EL VÉRTICE ESTÁ FUERA DEL PAPEL

Si tenemos dos rectas r y s que se cortan en un punto, pero que nos queda fuera del papel y queremos determinar su bisectriz:

PASOS:

Dibujamos una recta cualquiera t que corte a las dos rectas r y s, formando con ellas los ángulos A, B, C y D.
Hacemos las bisectrices de los 4 ángulos.
Donde se cortan las bisectrices determinan los puntos M y N.
Si uno los puntos M y N, obtengo la recta b, bisectriz del ángulo que forman r y s.

4. DIVISIÓN EN TRES DE UN ÁNGULO DE 90º

Necesitamos realizar la trisección del único ángulo del que es posible, el de 90º.

PASOS:

Dado un ángulo de 90º.
Hacemos centro de compás en el vértice del ángulo con la abertura que queramos y determinamos 1 y 2.
Haciendo centro de compás en 1 y 2 con la misma abertura determinamos los puntos 3 y 4.
Uniendo el vértice del ángulo con 3 y 4, hemos dividido el ángulo de 90º en tres ángulos de 30º.

5. ÁNGULO DE 75º

PASOS:

Trazo una recta perpendicular a la recta r por el punto V.
Hacemos centro de compás en el punto V del ángulo con la abertura que queramos y determinamos 1 y 2.
Haciendo centro de compás en 1 con la misma abertura determinamos el punto 3.
Uno 3 con V.
Hago la bisectriz del ángulo determinado.
Uniendo el punto 4 con V obtengo el ángulo de 75º.

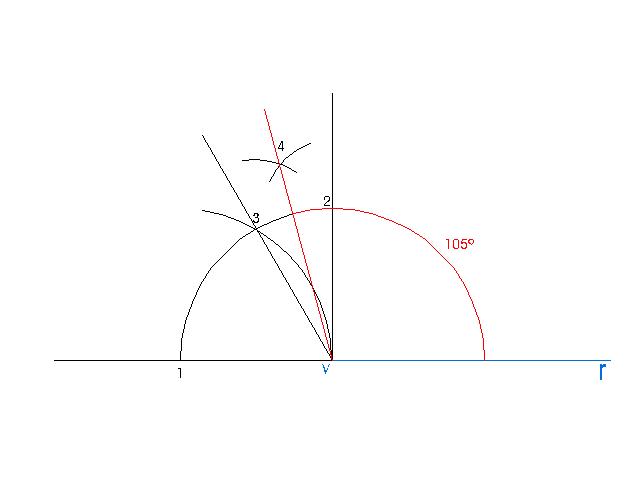
6. ÁNGULO DE 105º

PASOS:

Trazo una recta perpendicular a la recta r por el punto V.
Hacemos centro de compás en el punto V del ángulo con la abertura que queramos y determinamos 1 y 2.
Haciendo centro de compás en 1con la misma abertura determinamos el punto 3.
Uno 3 con V.
Hago la bisectriz del ángulo determinado.
Uniendo el punto 4 con V obtengo el ángulo de 105º.