El grabado. Técnicas.

El grabado. Técnicas

Reportaje fotográfico. Ejemplo Dora Maar y Picasso con el "Guernica"

Reportaje fotográfico

Historia de la fotografía

Historia de la fotografía

La primera fotografía de la historia que se conserva fue tomada en 1826 por el ingeniero francés Nicéphore Niépce desde la ventana de su granero de Saint Loup de Varennes, en Francia.

Tipos de planos, angulaciones y profundidad de campo

Tipos de planos, angulaciones y profundidad de campo

Esquema para el análisis de un anuncio publicitario

Esquema para el análisis de un anuncio publicitario

Estrategias creativas en la publicidad: el catálogo kickstart.

Estrategias creativas en la publicidad

Publicidad. El arte de convencer

Presentación sobre el tema de la publicidad. Unidad El arte de convencer

Teoría del cómic

La composición

Apuntes sobre la composición artística

TÉCNICAS GRÁFICO-PLÁSTICAS DE PINTURA

Elementos del lenguaje gráfico-plástico

Apuntes del lenguaje gráfico-plástico

Esquemas compositivos

Esquemas compositivos

Colores fríos y cálidos

                                                               Contrastes de Johannes Itten

TEORÍA DEL COLOR 1

  

Empezaremos diciendo que el color en sí no existe, no es una característica del objeto, e s más bien una apreciación subjetiva nuestra. Por tanto, podemos definirlo como, una sensación que se produce en respuesta a la estimulación del ojo y de sus mecanismos nerviosos, por la energía luminosa de ciertas longitudes de onda. El color es pues un hecho de la visión que resulta de las diferencias de percepciones del ojo a distintas longitudes de onda que componen lo que se denomina el "espectro" de luz blanca reflejada en una hoja de papel. Estas ondas visibles son aquellas cuya longitud de onda está comprendida entre los 400 y los 700 nanómetros; más allá de estos límites siguen existiendo radiaciones, pero ya no son percibidos por nuestra vista. Lo que ocurre cuando percibimos un objeto de un determinado color, es que la superficie de ese objeto refleja una parte del espectro de luz blanca que recibe y absorbe las demás. La luz blanca está formada por tres colores básicos: rojo intenso, verde y azul violeta. Por ejemplo, en el caso de objeto de color rojo, éste absorbe el verde y el azul, y refleja el resto de la luz que es interpretado por nuestra retina como color rojo. Este fenómeno fue descubierto en 1666 por Isaac Newton, que observó que cuando un haz de luz blanca traspasaba un prisma de cristal, dicho haz se dividía en un espectro de colores idéntico al del arco iris: rojo, anaranjado, amarillo, verde, azul, añil y violeta.

 

Otras definiciones de color:

 -Sensación producida por los rayos luminosos que impresionan los órganos visuales y que depende de la longitud de onda.

-Propiedad de la luz transmitida, reflejada o emitida por un objeto, que depende de su longitud de onda.

CÍRCULO CROMÁTICO (Círculo de los Colores):

El Círculo Cromático engloba prácticamente todos los colores existentes, pero la cualidad es que ayuda a entender la relación entre ellos, las mezclas necesarias para formar un color, las variables de intensidad o saturación, primarios y secundarios, cálidos y fríos, etc.

COLORES PRIMARIOS:

Colores: Rojo magenta, Azul cyan, Amarillo limón.

Posible definición: Son los que no resultan de la mezcla de otros colores. Se pueden mezclar entre sí para producir la mayoría de los colores.

COLORES SECUNDARIOS:

Colores: Violeta, Anaranjado, Verde

Posible definición: Son los colores generados a partir de las mezclas de los primarios.

 

COLORES CÁLIDOS Y FRÍOS:

Los colores no tienen temperatura en sí, pero históricamente se ha hecho una asociación, que puede tener que ver con asociaciones según objetos o elementos de la naturaleza, como lo son las estaciones del año y sus colores asociados.

 

 

 

MATIZ O TONO

Fragmento de color “neutro”, o sea, sin sumar blanco ni negro.

SATURACIÓN O BRILLO

Fragmento de color neutro con agregado de blanco o negro. También llamado intensidad.

 

 

CONSTRUCCIÓN DE POLIEDROS CON CARTULINA

http://www.matematicasvisuales.com/html/geometria/construccionpoliedros/cartulina2.html

MOVIMIENTOS Y TRANSFORMACIONES EN EL PLANO

Movimientos y transformaciones en el plano

http://docentes.educacion.navarra.es/msadaall/geogebra/movimientos.htm

	Traslación			Figuras con ejes de simetría Ejemplo 1 Ejemplo 2 Ejemplo 3 Ejemplo 4		Composición de traslaciones
	Simetría axial			Figuras con simetría de giro Ejemplo 1 Ejemplo 2 Ejemplo 3 Ejemplo 4		Composición de dos simetrías
	Giro			Generador de logos con simetrías de giro		Composición de dos giros Con el mismo centroCon centro diferente
	Simetría central			Movimientos en las teselaciones de Escher		Giro con traslación
	Homotecia			Jugando con la simetría axial		Otras composiciones

CONSTRUCCIONES GEOMÉTRICAS CON REGLA, COMPÁS Y ESCUADRA

En la siguiente dirección podemos encontrar construcciones geométricas.

http://docentes.educacion.navarra.es/msadaall/geogebra/reglaycompas.htm

Construcciones geométricas con sólo regla y compás							Construcciones geométricas con regla, compás... y escuadra
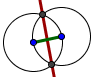	Mediatriz de un segmento		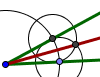	Bisectriz de un ángulo		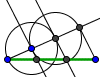		Trisección de un ángulo
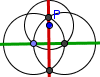	Perpendicular a una recta por un punto dados		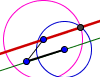	Paralela a una recta por un punto dados		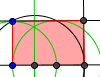		Rectángulo aúreo
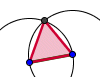	Triángulo equilátero		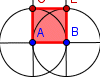	Cuadrado 1 Cuadrado 2				Cuadrado
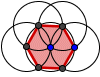	Hexágono regular Hexágono regular 2		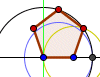	Pentágono regular				Pentágono regular

CUADRILÁTEROS

Resulta un tanto difícil hacer una clasificación de los cuadriláteros, por lo que como introducción a este tema, cito textualmente la definición de cuadriláteros que hace Euclides en su libro “Los Elementos”

“Definición 22. De los cuadriláteros, cuadrado es el que tiene los lados iguales y los ángulos rectos; rectángulo el que es rectangular pero no equilátero; rombo el que es equilátero, pero no tiene los ángulos rectos; y romboide el que tiene los lados y los ángulos opuestos iguales, pero ni es equilátero ni tiene los ángulos rectos. Los otros cuadriláteros se llaman trapecios.”

Un cuadrilátero  es un polígono que tiene 4 lados.  Los cuadriláteros pueden tener distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales, y la suma de sus ángulos internos siempre da como resultado 360º.

Existen cuadriláteros simples y cuadriláteros complejos. Sólo vamos a estudiar los cuadriláteros simples, aquellos cuyos lados no se cortan:

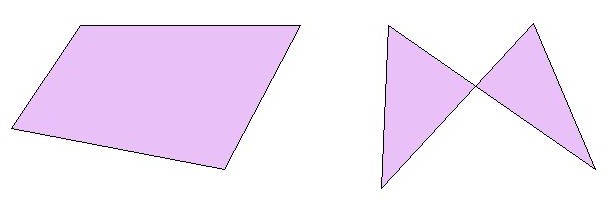
Clasificación de los cuadriláteros

Los cuadriláteros se dividen en cuadriláteros convexos y cuadriláteros cóncavos.
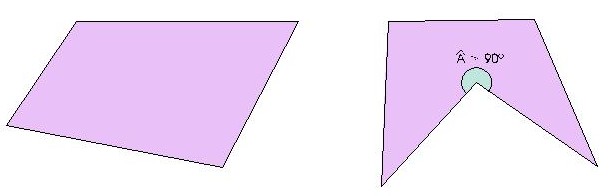
Un cuadrilátero es convexo, cuando ninguno de sus ángulos interiores es mayor de 90º.
Un cuadrilátero es cóncavo, cuando uno de sus ángulos interiores es mayor de 90º.

Cuadriláteros convexos

PUNTOS Y RECTAS NOTABLES DE UN TRIÁNGULO

En el siguiente enlace podemos encontrar una aplicación interactiva sobre las rectas notables.

 

 

http://docentes.educacion.navarra.es/msadaall/geogebra/triangulos.htm

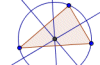	Mediatrices y Circuncentro		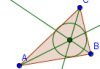	Bisectrices e Incentro
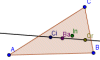
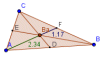	Medianas y Baricentro		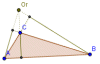	Alturas y Ortocentro
	Centros de un triángulo y Recta de Euler

TEMA: RECTAS NOTABLES DE UN TRIÁNGULO

TRIÁNGULOS

TEMA 4: TRIÁNGULOS

Un triángulo (ABC) es una figura plana limitada por tres rectas que se cortan dos a dos en tres puntos, no alineados, determinando los segmentos (a, b y c) que son los lados del triángulo. Para que tres segmentos formen un triángulo ABC es necesario que cada uno de ellos sea menor que la suma de los otros dos y mayor que su diferencia.

La suma de los ángulos internos de un triángulo es de 180º.

Nomenclatura de los triángulos

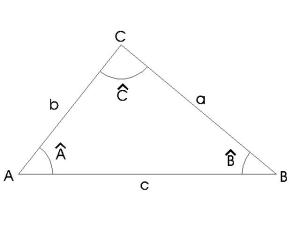
• Los vértices del triángulo se nombran con letras mayúsculas (A, B, C)
• Los lados del triángulo se nombran con la letra minúscula de su vértice opuesto (a, b, c)
• Los ángulos del triángulo se denominan con la letra mayúscula del vértice que los forma y el símbolo de ángulo (^).